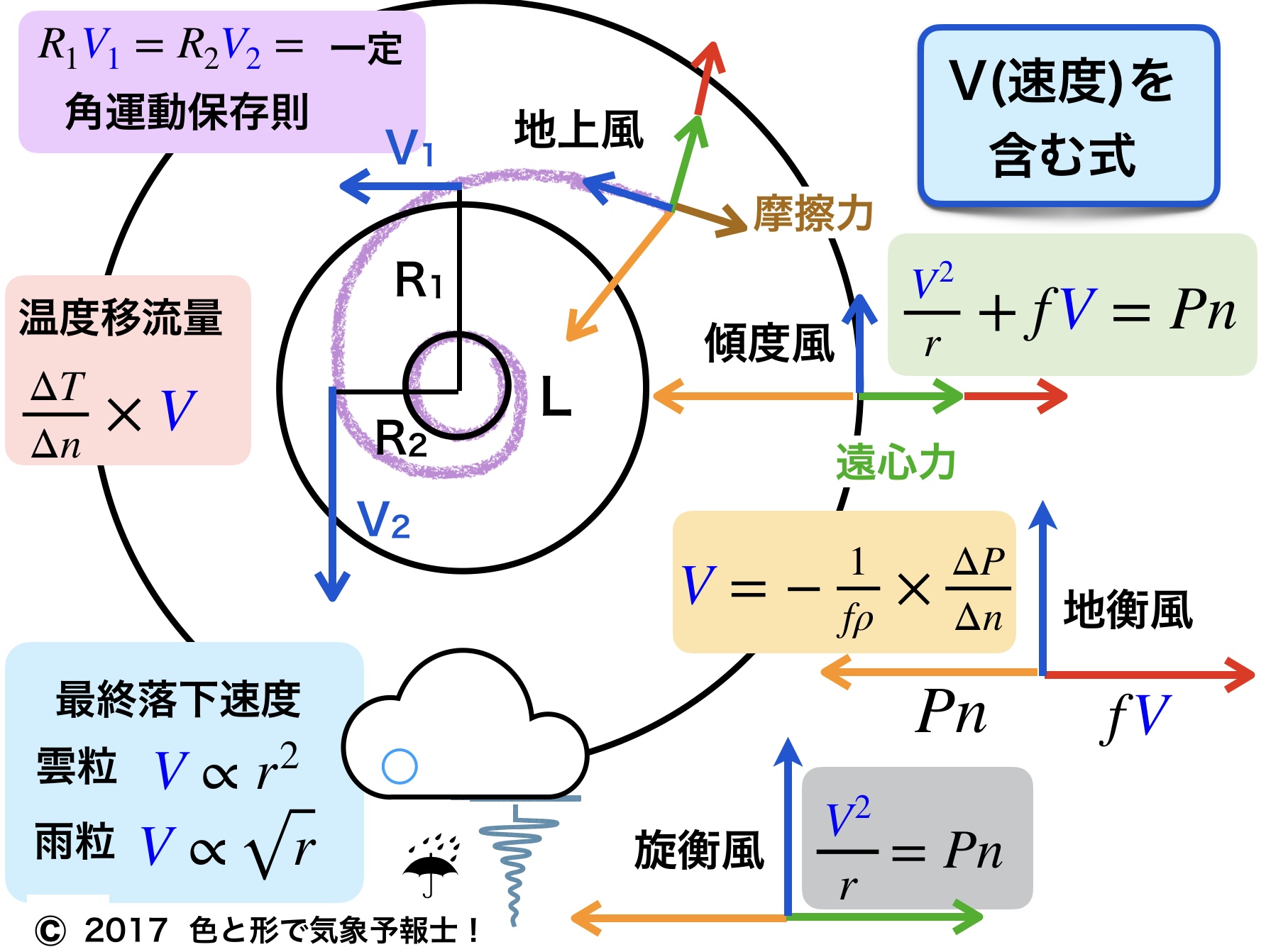
気象予報士試験の勉強をしていると V (風速、落下速度)を含む式がよく出てきます。あっちこっちの分野でVが出てきて、ごっちゃごっちゃになりそうです。
ということで、主な式を一つの模式図にまとめました。おなじみの式ばかりですが一つ一つ簡単に説明します。
目次
1.地衡風
図の右側、下から2番目の式です。
1-1. 気圧傾度力の式
気圧傾度力の式には気圧差を使う方法と高度差を使う方法の2種類あります。
Pn:気圧傾度力[N/kg] ρ:密度[kg/m3] ΔP:気圧差[Pa] Δn:距離差[m] Δz:高度差[m] g:重力加速度[m/s2]とすると
◆ 気圧差を使う式
$$\mathit{P_{n}=-\frac{1}{ρ}\frac{ΔP}{Δn}}$$
◆ 高度差を使う式
$$\mathit{P_{n}=-g\frac{Δz}{Δn}}$$
1-2. コリオリ力の式
F:コリオリ力 [N/kg]
f:コリオリパラメータ V:速度
$$\mathit{F=fV}$$
コリオリパラメータの式は以下になります。
$$\mathit{ f }\mathrm{ =2ΩsinΦ}$$
1-3. 地衡風の式
◆ 気圧差を使う式
$$\mathit{V=-\frac{1}{fρ}×\frac{ΔP}{Δn}}$$
◆ 高度差を使う式
$$\mathit{V=-\frac{g}{f}×\frac{Δz}{Δn}}$$
高度差を使う式については静力学平衡(静水圧平衡)から導き出す方法もありますが、詳しいことは各テキストで確認してください。
2.傾度風
図にある円は低気圧の等圧線をイメージしたものです。図の右側にあるのが傾度風の式です。
傾度風は気圧傾度力・コリオリ力・遠心力がつり合った状態で吹く風で、主に高気圧や低気圧の周囲で吹いている風です。
2-1. 遠心力
遠心力の式にもV(速さ)が出てきます。
半径を r とすると
$$遠心力=\mathit{\frac{V^2}{r}}$$
2-2. 傾度風の式
$$\mathit{\frac{V^2}{r}+fV=P_n}$$
3.地上風
図の傾度風の左上に地上風のベクトルがあります。
地衡風・傾度風は上空での風ですが、地上・海上では摩擦力によって風の向きと強さが変わります。
風は気圧の低い方へ等圧線と交差して吹きます。地上風を表す式もありますが、ここでは省略します。
4.旋衡風
図の右下にある旋衡風は竜巻の風です(台風の中心付近の風も旋衡風と見る人もいるようです)。
竜巻は高気圧・低気圧などに比べるとずっとスケールの小さな現象です。
そのためコリオリ力が働かず気圧傾度力と遠心力のバランスが取れた状態で吹きます。式にするとこのようになります。
$$\mathit{\frac{V^2}{r}=P_n}$$
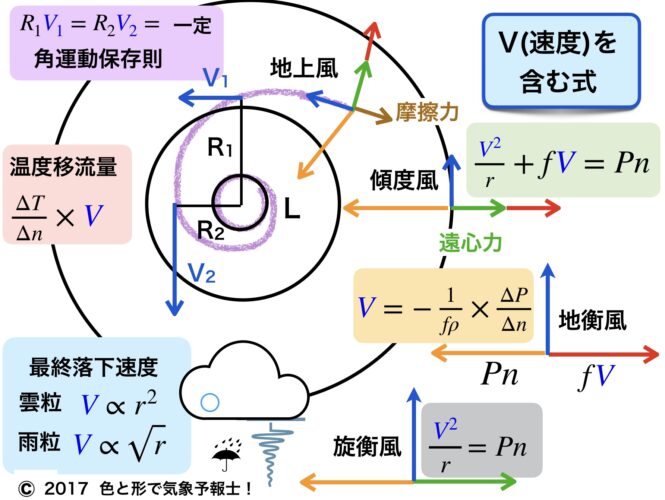
5.角運動量保存則
5-1. 風は中心の方が強い
図の左上に移ります。低気圧内の地上風は低気圧の中心に近づくような方角で吹きます。
ここで風を空気塊として考えてみます。一つの空気塊が次第に低気圧の中心に近づいていくとします。
ここで4択です。空気塊が移動する速さは中心に近づくに従って①速くなる②遅くなる③変わらない④分からない、どれでしょうか?
答えは ①速くなる です。ここで登場するのが角運動量保存則です。
角運動量保存則とは「回転する物体の回転半径と回転速度をかけた数値は一定に保たれる」という法則です。風に当てはめると、回転半径が中心からの距離、回転速度が風速になります。
この法則を式にするとこうなります。
R:回転半径 V:回転速度 として
$$R_1V_1=R_2V_2=一定$$
例えば、図の低気圧(台風とします)の中心から R1 の距離で風速V1の風が吹いていたとします。
この風が中心に近づいて行き、中心からの距離がR1の 1/2 である R2 になったとします。
このとき、風速V2 はV1の2倍になるということです。
5-2. 風は中心の方が弱い
ここまでの説明で おやっ?っと思った人もいるかもしれません。
傾度風のところで、低気圧性循環の場合、遠心力とコリオリ力を足した力が気圧傾度力と等しいと学びました。
ところで、遠心力は低気圧の中心に近い方が強くなります。遠心力が大きくなると、その分コリオリ力は弱くなり風も弱くなるはずです。
中心に近い方が風が強くなるという角運動量保存則と矛盾しているように思えます。
これは次のように考えれば理解できます。
角運動量保存則が当てはまるのは一つの空気塊がだんだん中心に近づいて行くことを想定しています。
一方、傾度風のところで比較したのは複数の別個の空気塊です。例えば、中心に近いところにある空気塊と離れたところにある空気塊が「よーいドン」で一斉にスタートしたときに、どっちが速く進むかということです。
さらに言えば、傾度風が低気圧中心に近い方が弱いというのは、気圧傾度がどこも同じという仮定の上の理屈です。台風に関して言うなら中心に近いほど等圧線が込み合って気圧傾度が大きくなっている、だから中心に近いほど風速が大きくなるといえます。
6.温度移流量
これに関しては詳しい説明は省略します。式は次の通りです。
2つの地点に関し、ΔT:気温差 Δn:距離
V:2地点間を吹く風の風速 とすると
$$温度移流量=\mathit{\frac{ΔT}{Δn}×V}$$
7.最終落下速度
雲粒や雨粒が落下するとき、ある時点で重力と空気抵抗力が等しくなり、落下速度が一定になります。この時の速度が最終落下速度(終端速度)です。
速度そのものの式は複雑なので、比例関係を表す式を紹介します。
V:落下速度 r:粒の半径 とすると
◇ 雲粒の場合:
$$\mathit{V∝r^2}$$
◇ 雨粒の場合:
$$\mathit{V∝√r}$$
図に載せた式の説明は以上になります。しっかり覚えて応用問題にも対応できたらいいですね。