今回は水蒸気密度、水蒸気圧に関係する飽和状態、混合比、露点温度の意味と混合比等の性質について相関図を使って考えていきます。
冒頭のイメージ図はこれから取り上げる内容を全部ひっくるめて一つにまとめたものです。ごちゃごちゃっとしていますが、これから幾つかの図に分割して考えていきます。
また、6つの水分量(水蒸気量)表現方法が互いにどのような関係にあるかを1つの図にまとめた記事もあるので、そちらもご覧ください。
1.飽和と露点温度の意味
飽和と露点温度についてはこれまで何回か取り上げてきたので簡単に復習します。
◆ 飽和とは空気に水蒸気が限界まで含まれている状態のことです。
そして大切なのは飽和水蒸気密度、飽和水蒸気圧は温度だけの関数、つまり温度にのみ依存しているということです。
◆ 露点温度とは圧力を一定に保ったまま未飽和の湿潤空気の温度を下げていき、水蒸気が凝結を始める時の温度のことです。
水蒸気が凝結を始める時というのは、つまり空気が飽和に達した時といえます。
ただし、空気塊が上昇して断熱冷却によって飽和したときの温度は気圧が変化しているので、上昇前の空気塊の露点温度とはいえません。
2.露点温度が定まる状態
これから、どのような条件が整った時の温度が露点温度となるか考えます。次の図の左側をご覧ください。
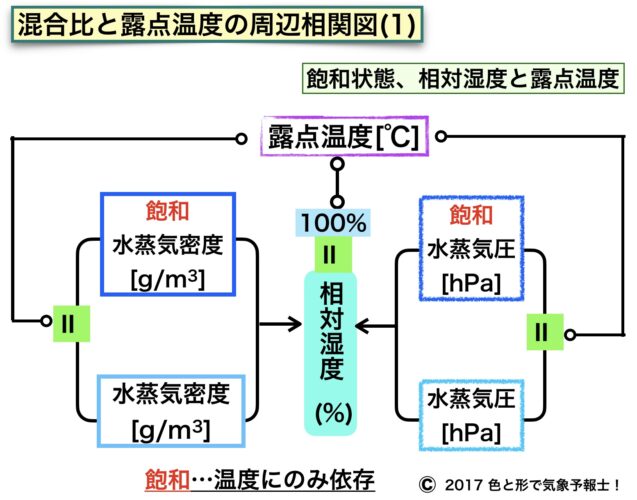
2-1. 水蒸気密度から
空気中の水分量の表現する一つの方法は水蒸気密度です。単位は g/m3 です。
露点温度の定義を当てはめるなら湿潤空気が初めて次の状態になった時の温度が露点温度になります。
水蒸気密度[g/m3] = 飽和水蒸気密度[g/m3]
2-2. 水蒸気圧から
水分量の表現のもう一つの方法は水蒸気圧です。単位はhPa です。
水蒸気密度と同様に考えれば次の等式が成り立った時の温度が露点温度です。
水蒸気圧[hPa] = 飽和水蒸気圧[hPa]
2-3. 相対湿度から
相対湿度(%)は天気予報で出てくるいわゆる湿度のことで次の2つの方法で求めます。
◆ 水蒸気密度 ÷ 飽和水蒸気密度×100
◆ 水蒸気圧 ÷ 飽和水蒸気圧×100
相対湿度が100%になった時の温度が露点温度です。
3.混合比の求め方
3-1. 水蒸気密度から
混合比とは湿潤空気に含まれる水蒸気質量と乾燥空気質量の比をいい、次の式で求めます。
$\color{blue}混合比W[g/kg]=\Large{\frac{水蒸気質量[g]}{乾燥空気質量[kg]}}$
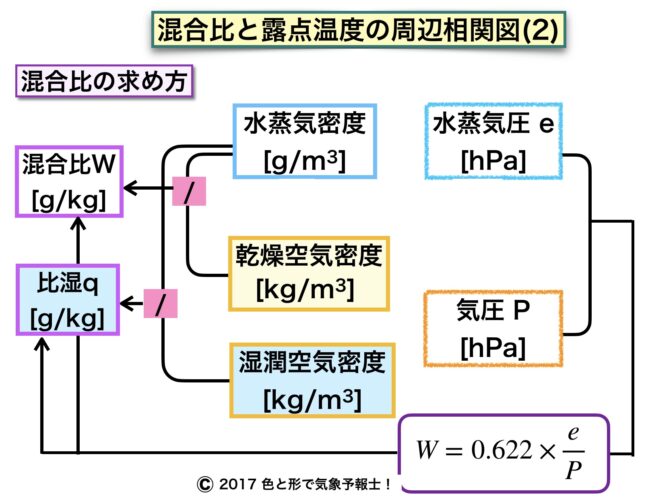
「相関図(2)」から説明します。図では水蒸気量と乾燥空気量を質量ではなく密度で示していますが、計算で単位体積は消去されるので同じことです。
また、乾燥空気密度ではなく湿潤空気密度を分母とすれば比湿を求めることができます。
混合比と比湿の値の差は非常に小さいので、ここでは全て混合比について記述します。
3-2. 水蒸気圧から
図の右側を見てください。水蒸気圧から混合比を求めるには次の式を用います。
水蒸気圧をe、気圧をP、混合比をw として
$\color{blue}W=0.622×\Large{\frac{e}{P}}$
この式も混合比、比湿、どちらにも用いることができます。
この 0.622 という数字は水蒸気の分子量18を乾燥空気の分子量28.96 で割った値です。
4.露点温度が定まる状態 <飽和混合比から>
下の「周辺相関図(3)」から説明します。
4-1. 飽和混合比の求め方
■ 水蒸気密度から
飽和混合比は飽和した時の混合比です。次の式で求まります。
$\color{blue}飽和混合比W[g/kg]=\Large{\frac{飽和水蒸気質量[g]}{乾燥空気質量[kg]}}$
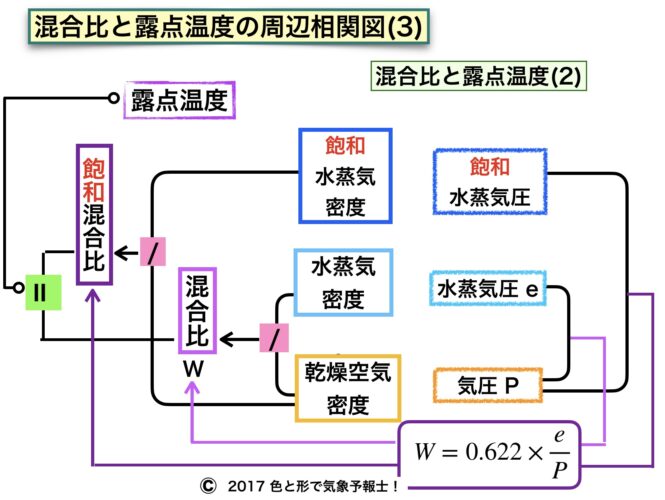
■ 水蒸気圧から
水蒸気圧e を飽和水蒸気圧に置き換えれば、先ほどの式を使って飽和混合比を求めることができます。
4-2. 露点温度が定まる状態 <飽和混合比から>
混合比と飽和混合比が等しくなった時の温度が露点温度になります。
以上をまとめたのが冒頭の図です。
おまけになりますが、露点温度と実際の温度との差が湿数です。湿数が小さいほど空気が湿っていることになります。
5.露点温度と混合比の相関図から分かること
◎ 飽和水蒸気密度と飽和水蒸気圧は温度にのみ依存する
◎ 水蒸気密度は単位体積当たりの質量なので、断熱膨張などで体積が変われば値が変わる
◎ 混合比は凝結や蒸発がない限り、体積や温度が変わっても一定(保存される)
◎ 混合比は温度と関係ないが、飽和水蒸気密度、飽和水蒸気圧は温度と関係するので飽和混合比は温度によって変わる
◎ 断熱膨張などにより気圧が変われば分圧である水蒸気圧も変わる
もし、不正確なところがあれば追って修正します。
水分量の表現のところはちょっとひねった問題が出されると結構焦りますが、基本をしっかり押さえておきたいものです。
