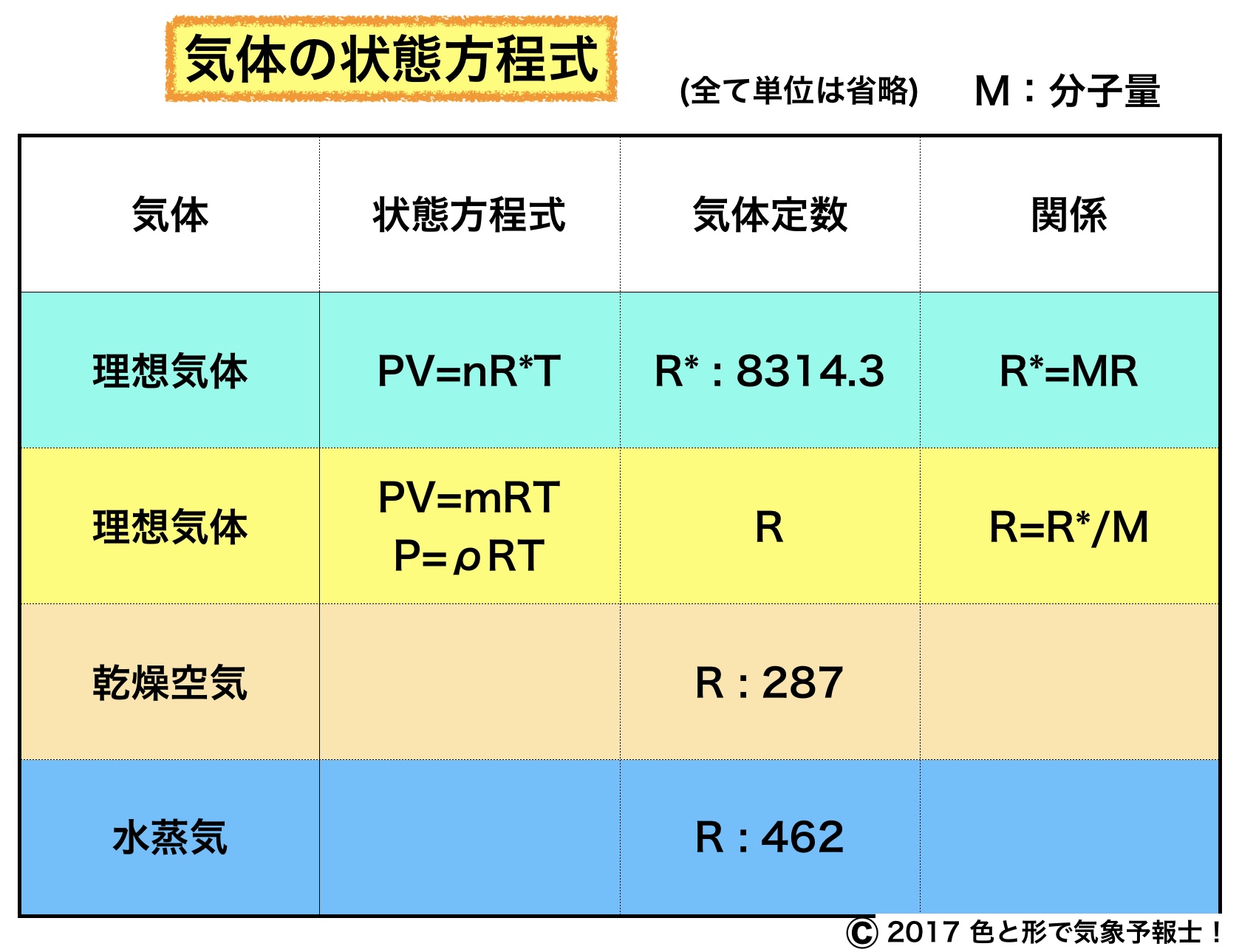
以前の記事で単位としてモルを使い、気体の種類を問わずに表せる気体の状態方程式と普遍気体定数について学びました。
今回は単位として質量を使い、気体の種類で使い分ける気体の状態方程式と気体定数を学びます。まずはここまでの流れを整理します。
■ 熱力学にかかわる基本的な用語の確認
⇒「気体分子と圧力の関係」
■ 圧力を主体にした時の温度、体積、分子数の関係
⇒「気体分子と圧力の関係」
■ 体積を主体にした時の温度、圧力の関係(ボイル・シャルルの法則)
⇒「気体分子と体積の関係」
■ 体積と分子数の関係(アボガドロの法則)
⇒「気体分子と体積の関係」
■ 理想気体の状態方程式(気体の種類によらない式)
■ 理想気体の状態方程式(気体ごとの式)(←今回の記事)
まずは復習から。。
1.理想気体の状態方程式と普遍気体定数
理想気体とはボイル・シャルルの法則が厳密に成り立つ気体です。
P : 圧力 V:体積 T:絶対温度
n[kmol] : 気体の量 (キロモル)
R* : 普遍気体定数(気体の種類に無関係)とすると
PV=nR*T です。
普遍気体定数R* の値は 8314.3JK-1kmol-1 です。
2.気体の状態方程式
今度は気体の種類によって気体定数が変わる場合を考えます。
2-1. 質量で表す場合
既に取り上げた方程式 PV=nR*T では 気体の種類に関係なく使える n[mol] を用いています。
今回は、気体ごとで異なる質量 m[kg] を用いた式について考えます。
気体の圧力をP[Pa]、体積をV[m3]、質量をm[kg]、温度をT[K]、その気体における気体定数をRとします。(注:m は長さの単位つまりメートル、m は質量の記号です。)
すると、次の式が成り立ちます。
PV=mRT
これを理想気体の状態方程式といいます。
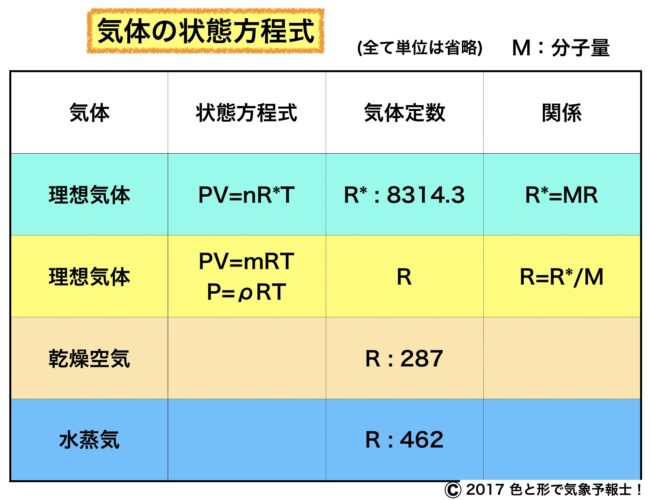
2-2. 密度で表す場合
密度と次に出てくる比容の記号と単位については「気象学における物理量と単位(1)」を参照してください。
密度は単位体積当たりの質量です。記号は ρ(ロー)、単位は kg・m-3 です。
ですから密度 ρはm/V=m・V-1で表せます。
先ほどの気体の状態方程式 PV=mRT を変形すると
P=m/V×RT となり、m/V をρで置き換えると
P=ρRT となります。
この式から圧力Pは空気密度ρと絶対温度Tに比例することが分かります。
この式の覚え方のイラストが本文の終わりにあります。
2-3. 比容で表す場合
比容は密度とは逆で、単位質量当たりの体積をいいます。
記号は α(アルファ)、単位は m3・kg-1 です。
比容は、単位が密度の逆数なので α=1/ρ、さらに変形すると ρ=1/αとなります。これをP=ρRT に代入すると、
P=1/α×RT → Pα=RT →
α=RT/P となります。
この式から比容αは絶対温度Tに比例し、圧力Pに反比例することが分かります。
3.気体定数と気体の分子量
ここで1キロモルの気体を考えます。
3-1. モル数を用いた状態方程式によると
PV=nR*t → この場合、1kmol なので、n=1 となり
PV=R*T (1) となります。
3-2. 質量を用いた状態方程式によると
PV=mRT → この場合、1kmol なので質量m[kg] はその気体の分子量M[kg×kmol-1] の数値に等しくなり
PV=MRT (2) となります。
(1)と(2) を結びつけると
PV=R*T=MRT となります。
この式から、ある気体に固有な気体定数R と普遍気体定数R*との関係は次のようになることが分かります。
R*=MR ⇒
R=R*/M
ですから、気体の分子量が分かれば気体定数R を求めることができます。
また、気体定数R の値はその気体の分子量に反比例することが分かります。
さらに、R=R*/M から気体の状態方程式は次の式でも表せます。
$PV=m\large{\frac{R^*}{M}}T$
4.乾燥空気の気体定数
気象学では水蒸気を除いた乾燥空気(窒素、酸素、アルゴンなどの混合気体)の気体定数を多用します。
ここからは乾燥空気の平均分子量を28.96 として計算します。
● 1mol の乾燥空気 ⇒ 28.96g
● 1kmol の乾燥空気 ⇒ 28.96kg
● 乾燥空気の気体定数 Rd を計算すると
Rd = R*/M = 8314.3JK-1kmol-1 / 28.96kgkmol-1
≒ 287JK-1/kg = 287JK-1kg-1
となります。
つまり、乾燥空気の気体定数は 287JK-1kg-1 です。
これは、乾燥空気1kg を1K上昇させるために、287Jの熱量が必要ということを表します。
5.水蒸気の気体定数
水蒸気(H2O) の分子量を18として水蒸気の気体定数Rw を計算すると、
Rw=R*/M=8314.3JK-1kmol-1 / 18kgkmol-1
≒ 462JK-1kg-1 となります。
つまり、水蒸気の気体定数は462JK-1kg-1 です。
これは、水蒸気1kg を1K上昇させるために、462Jの熱量が必要ということを表します。
乾燥空気と水蒸気の気体定数の覚え方のイラストも記事の終わりに載せました。
6.乾燥空気と水蒸気の比較
気体定数で比べると
287JK-1kg-1(乾燥空気)< 462JK-1kg-1(水蒸気)となります。
気体定数は単位質量1kg の気体を1K上昇させるのに必要な熱量を示しているので、水蒸気の方が熱容量(比熱)が大きいことが分かります。
◇ 熱容量とは・・ ある物質の温度を1K上昇させるのに必要な熱量
◇ 比熱とは・・ 1g の物質の温度を1K上昇させるのに必要な熱量
水蒸気の方が熱容量が大きいことから、乾燥空気より暖まりにくく冷めにくいと理解できます。
実際の気象現象でも、乾燥空気より水蒸気を含む湿潤空気の方が暖まりにくく冷めにくいことが分かります。
これで熱力学分野の一つの山を越えました。この先、もう一つの山、熱力学の第一法則を学んでいきます。
最初の記事は「内部エネルギーとは」です。ちょっと寄り道して「気象学における物理量と単位」を読むのもいいかもしれません。
7.まとめ
▶ 気体の状態方程式・・PV=mRT
または P=ρRT
▶ 乾燥空気の気体定数・・ 287JK-1kg-1
▶ 水蒸気の気体定数・・462JK-1kg-1
8.覚え方の変なイラスト
8-1. 気体の状態方程式
おかしな図ですが、頭にPを乗せた老人ならぬ老蟻が手を広げています。
覚え方はP(P)は(=)老(ρ)蟻(R)手(T)
です。
8-2. 気体定数

老蟻が「じゃあな」と言って自分の城に帰るところです。
お尻に尻尾みたいな人参があって「野菜を知って!ミーだよ」みたいにアピールしています。
気体定数の覚え方は
じゃあな:乾燥空気は287
城に:水蒸気は462
野菜知ってミー:普遍気体定数は8314.3
てな具合です。
次は熱力学の第一法則に入ります。以前に取り上げた分野ですが、これからもっと詳しく掘り下げていくつもりです。お付き合いのほど、よろしくお願いします