地球が生命にとって一番気持ちいい温度になるためには温室効果なるものが必要です。
前回は大気の熱収支を考えましたが、今回 放射収支の視点から温室効果を考えます。
そのために、大気がある場合の地表の放射平衡温度を求め、さらに放射対流平衡によって、ついに丁度いい気温になる仕組みも考察します。
目次
1.温室効果のメカニズム
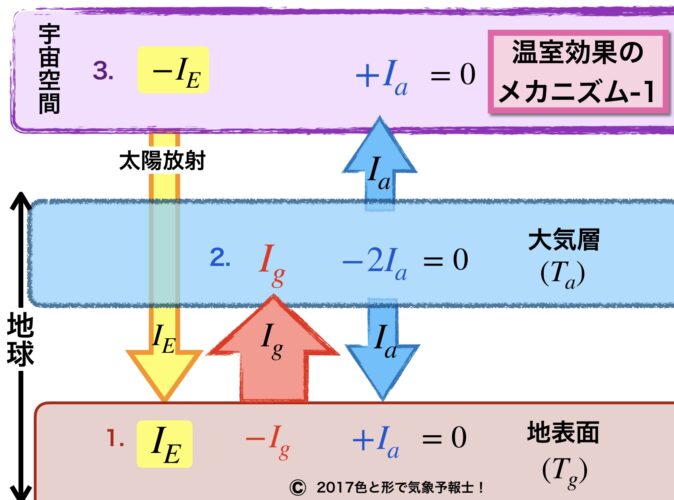
下記のイメージ図の説明をします。これは宇宙空間(大気上面)、地球大気、地表面の間の放射のやり取りを数式を用いて示したものです。少し説明を加えます。
1-1. 絶対温度 T
◎ 大気層の絶対温度:Ta
◎ 地表面の絶対温度:Tg
1-2. 3種類の放射エネルギー I
◎ 入射太陽放射エネルギー(黄色の矢印):IE
ここでは計算を簡略化するために、大気による吸収が0であると仮定します。
◎ 地表面放射エネルギー(ピンクの矢印):Ig
全て大気に吸収されると仮定します。
◎ 大気放射エネルギー(水色の矢印):Ia
大気は吸収した放射エネルギーを宇宙空間と地表面の両方に放出します。
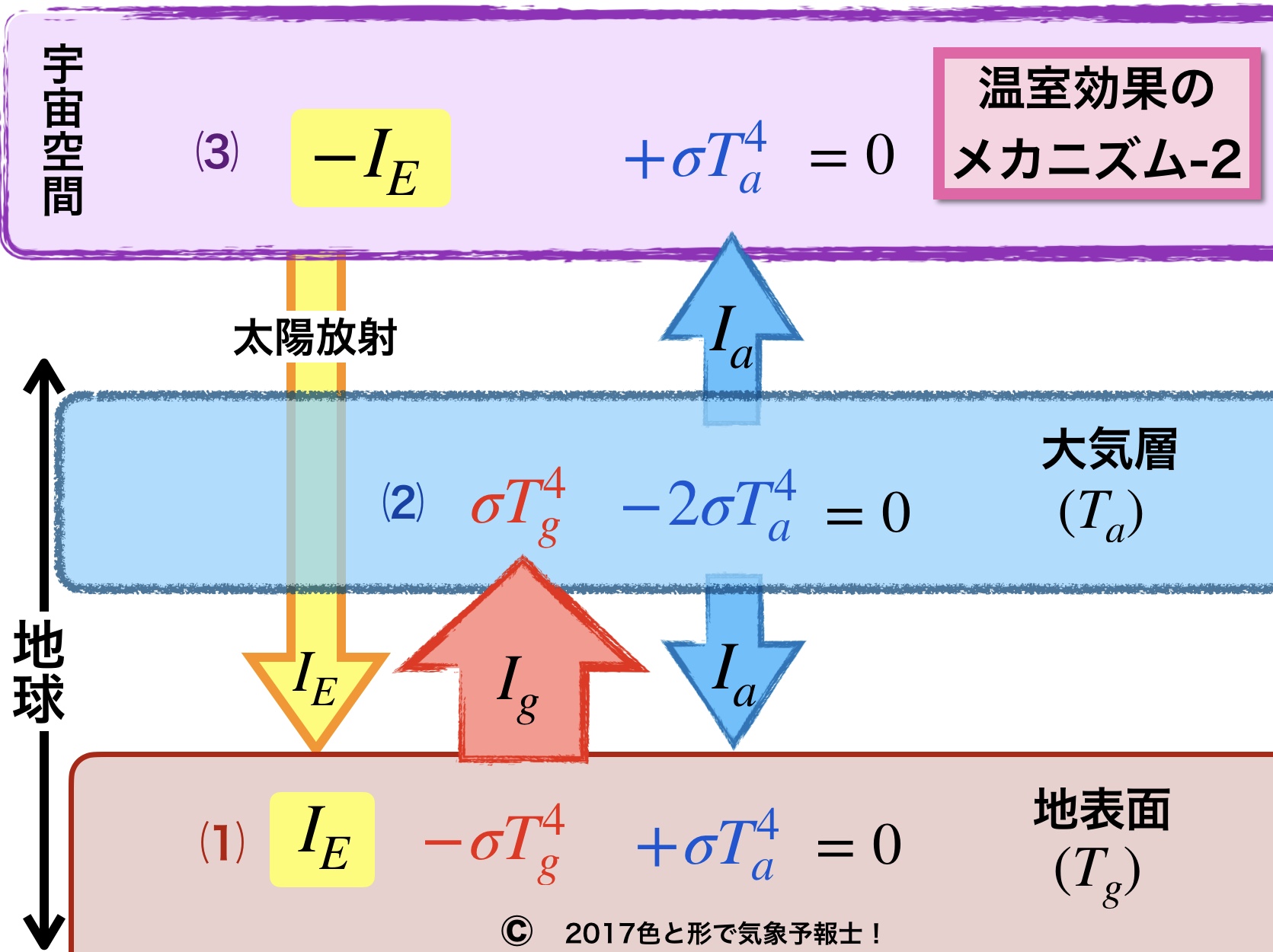
1-3. 放射収支の式
それぞれの放射収支の式は上記図の 1. ~ 3. です。プラスは吸収するエネルギー、マイナスは放出するエネルギーです。右辺が 0 なら放射平衡状態にあります。
3. の式は両辺に -1 をかけて、または式1. + 式2. で
IE -Ia = 0 さらに IE = Ia に変形できます。
1-4. ステファン・ボルツマンの法則を適用した式
ステファン・ボルツマンの法則を式にすると以下になります。
I = σT4
従って、地表面放射と大気放射は次のように表せます。
地表面放射:Ig = σTg4
大気放射:Ia = σTa4
すると上の「温室効果のメカニズム-1」の図は以下の図に置き換えることができます。
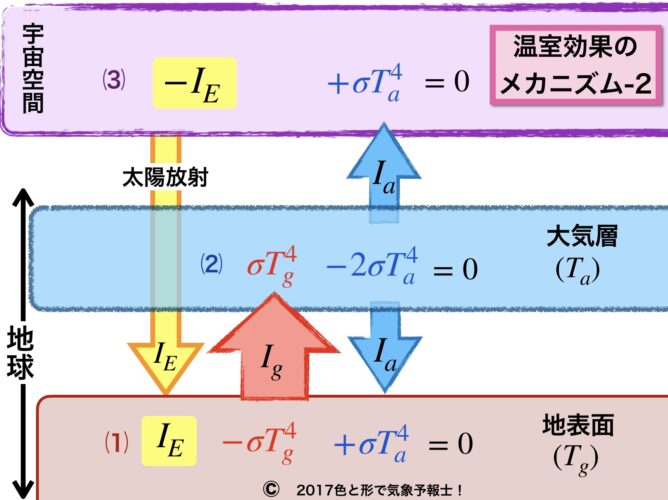
(3)の式は両辺に-1をかけて、または(1)+(2)で
IE - σTa4 = 0 さらに IE = σTa4 に変形できます。
1-5. 放射エネルギーの表現方法
地球の放射平衡温度を求める前に地球(この場合、大気層)に出入りする放射エネルギーの表し方を整理します。
地球が受ける太陽放射と地球が失う地球放射は同じ量になります。この点を踏まえると次の図にある関係が成り立ちます。
それぞれの関係について説明します。
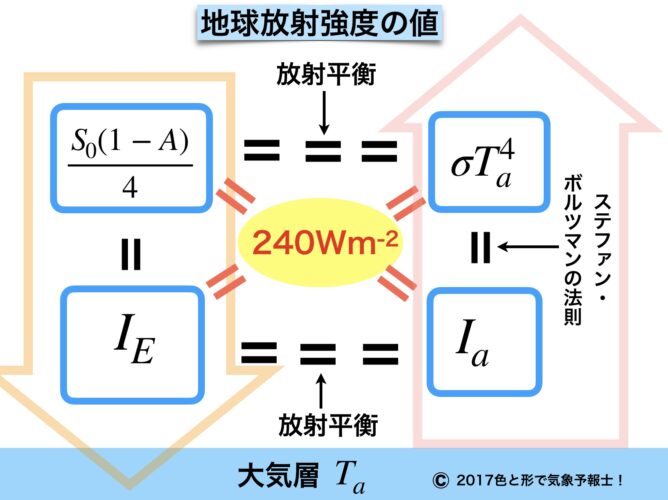
● IE = Ia ←放射平衡の関係
● Ia = σTa4 ←ステファン・ボルツマンの法則
● $\large{\frac{S_0(1-A)}{4}=I_E}$
以前の記事「放射平衡温度の求め方(放射7)」で次の式が成り立つことを示しました。
S0(1-A)= 4×IE 両辺を4で割れば上の式になります。
ただ、上記の記事では IE を地球放射強度として示していました。この記事では太陽放射エネルギーを IE 、地球放射エネルギーを Ia で表しています。ですから次の式も成り立ちます。
● $\large{\frac{S_0(1-A)}{4}}=I_a$ ←放射平衡の関係
でも、地球に入る太陽放射エネルギーと地球から出て行く地球放射エネルギーは平衡状態にあるので、上記の図のように IE を太陽放射エネルギーの記号としても結局は同じことです。
これまでの式により下の2つの式も成立します。
● $\large{\frac{S_0(1-A)}{4}=σT_a^4}$ ←放射平衡の関係
● IE = σTa4 ←放射平衡の関係
ここまでで、放射エネルギーの4つの表現方法が全てイコールで結ばれることが理解できました。
1-6. 地球放射強度の値
上記図の4つの表現方法のうち左上のものは定数の数値を代入して計算できます。
◇ 太陽定数:S0 = 1.37 × 103Wm-2
◇ アルベド:A = 0.3 従って
$\large{\frac{S_0(1-A)}{4}}$ = 240 Wm-2 となります。この値を
$\large{\frac{S_0(1-A)}{4}}$ = Ia に当てはめれば
Ia = 240 Wm-2 になります。これが地球放射強度になります。
1-7. 大気層の温度の求め方
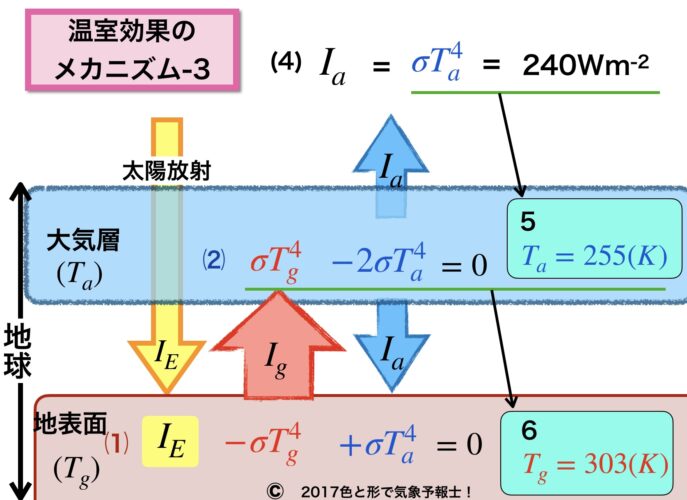
下のイメージ図をご覧ください。
Ia = σTa4 から σTa4 = 240Wm-2 ・・・(4)となります。
σ = 5.67 × 10-8Wm-2K-4 を代入すると
Ta = 255(K) ・・・5 となります。これが大気層の温度になります。
1-8. 地表面の温度の求め方
さらに上図の(2)の式 σTg4 - 2σTa4 = 0 にTa = 255 を代入すれば地表面の温度が導き出されます。
Tg = 303(K) ・・・6
303K=30℃ なので、大気がない場合の -18℃ より かなり暖かいですが、実際に観測される地表面の平均気温288K(15℃)と比べて高すぎる気温になっています。
1-9. 大気層が太陽放射の一部を吸収すると仮定
ここまでは、大気層は太陽放射を全く吸収しない、吸収率 0 と仮定して計算しました。
でも、多くのテキストでは、大気層における太陽放射の吸収率を 0.1 、地表面における太陽放射の吸収率を 0.9 として計算しています。
この場合、イメージ図のそれぞれの式は次のように置き換えられます。
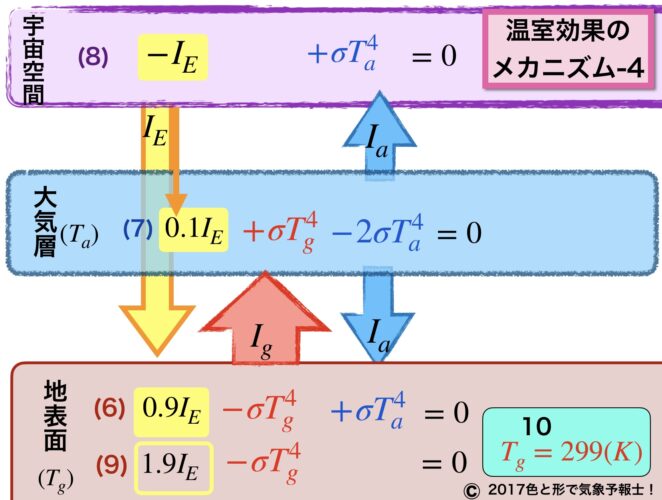
(6)を2倍して(7)と足すと σTa4 が消えて(9)になります。
IE = 240Wm-2 を式 (9) に当てはめて地表面の気温を算出すると、
Tg = 299(K) になります。
この値は大気層での太陽放射の吸収率を0と仮定した場合より低くなっています。それでも288Kよりはかなり高い気温です。
2.放射対流平衡
地表面の平均気温が299(K)より低くなる理由は大気の対流にあります。
それを示しているのが次のイメージグラフです。(これは「一般気象学」に掲載されているグラフを見ながら手作りしたもので厳密なものではありません)
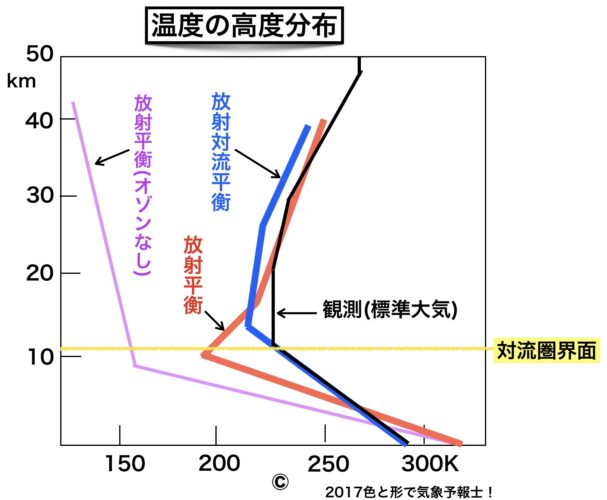
4つの線があります。順に説明します。
◆ 放射平衡(オゾンなし)(薄紫の線)
これはオゾン層がないと仮定した場合の分布の線です。地表面での気温は300K以上で、高度とともに気温は下がり続けています。
◆ 放射平衡(赤い線)
これはオゾンがある場合(実際にありますが)の分布の線です。
オゾンがない場合との違いは、対流圏界面から上空で再び温度が上昇している点です。これは成層圏にあるオゾンが太陽放射のうち、紫外線を吸収しているためです。
◆ 放射対流平衡(青い線)
放射平衡のグラフを見ると高度とともに急速に気温が下がっています。温度減率は観測値(1000mにつき6.5℃)と比べてかなり大きくなっています。
地表と上空の気温差が大きいと対流不安定になります。すると、地上の暖かい空気は上昇し、上空の冷たい空気は下降して、結果として高度による温度差が小さくなります。
加えて水蒸気を含んだ空気塊が上昇し雲の中で凝結する時、潜熱を放出することで周囲の大気を暖めます。こうして地上と上空の温度差が小さくなります。
このように放射に対流と潜熱の影響を加味したものが放射対流平衡です。
見て分かるように放射対流平衡の線が、対流圏内では最も現実の温度変化に近いものになっています。地表面の気温も観測値にほぼ等しくなりました。
◆ 観測(標準大気)(黒い線)
これは実際の温度分布の線です。
地表面の平均気温は288K(15℃)となり、やっと丁度いい温度になりました。(ここまで長かった…)
次回は散乱についてです。空が青い理由や虹の仕組みを学びます。お楽しみに!