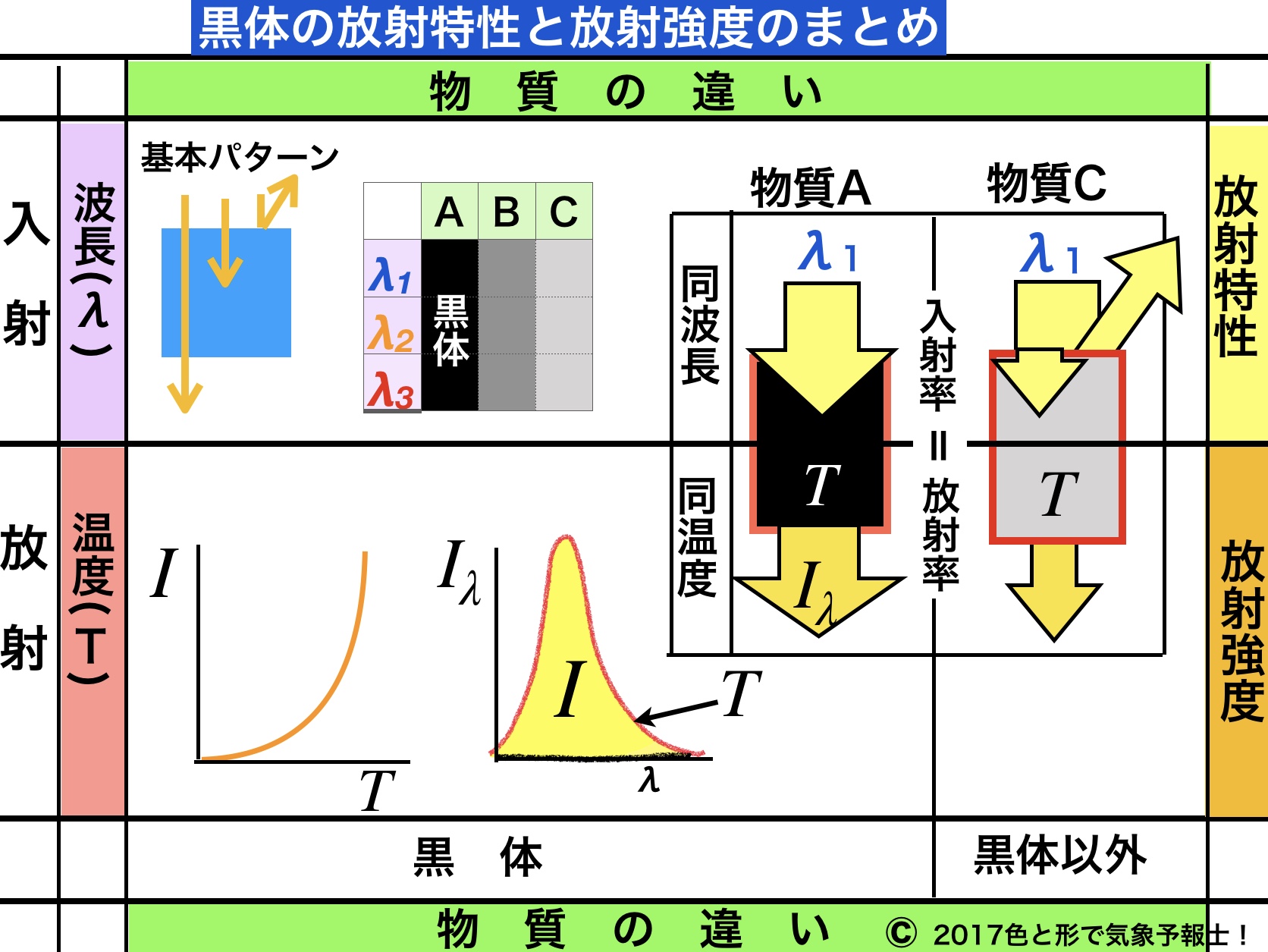
地球の温度が極端にならないためには地球に入るエネルギーと出ていくエネルギーのつり合いが保たれていなければなりません。
カギとなるのは黒体の性質です。太陽も地球も黒体であるゆえ、黒体に入る電磁波、黒体から出ていく電磁波の癖を知る必要があります。
基本的なことは「放射に関する法則(放射4)」にあるので、先にそちらを読んでもいいかもしれません。この記事では次の点に注目しながらさらに詳しく学びます。
◆ 黒体(地球)に入射した電磁波の行方(放射特性)
◆ 黒体(太陽と地球)から電磁波が放射されるときの仕組み(放射強度)
◆ 入射と放射の関係
冒頭のイメージ図はこれから順々に取り上げる内容を一つにまとめたものです。ごちゃごちゃしてて何だか分からないかもしれませんが、一つ一つ説明していきますので、お付き合いくだされば嬉しいです。
目次
1.黒体とは
黒体とは、すべての波長の放射を完全に吸収する仮想の物体のことです。
さらに、黒体は与えられた温度に応じた最大の放射エネルギーを射出します。これを黒体放射といいます。
太陽も地球もほぼ黒体とみなすことができます。
2.入射した電磁波の行方(放射特性)
物体に電磁波(放射)が当たった(入射した)とき、その電磁波は反射、吸収、透過、いずれかの道を選ぶことになります。
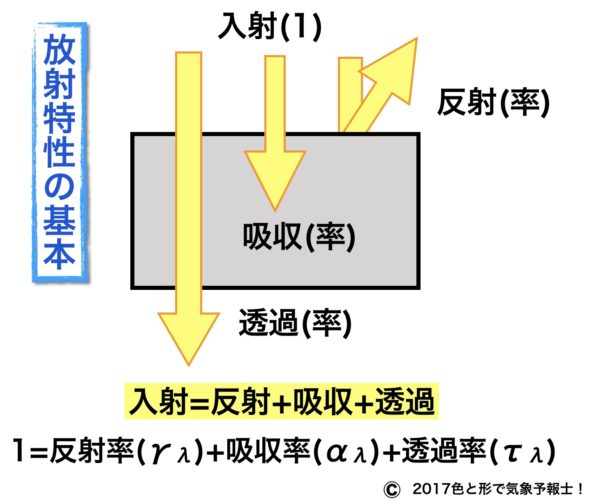
図にもありますが、反射量・吸収量・透過量を合計したものが入射量と等しくなります。
入射量=反射量+吸収量+透過量
さらに式の両辺を左辺(入射量)で割るとそれぞれを率で表すことができます。
$\ 1=反射率(\gamma_{\lambda})+吸収率(\alpha_{\lambda})+透過率(\tau_{\lambda})$
※ λ(ラムダ)は波長です。他のギリシャ文字の読み方は、γ:ガンマ、α:アルファ、τ:タウ です。
そして、反射量、吸収量、透過量の3つの量が、その物質の放射特性を表します。
3.放射特性を決める要素
3-1. 物質の性質
ある物質に電磁波が当たったとき、その電磁波がどのような放射特性を示すかは物質の性質により変わります。
例えば太陽からの可視光線が大気に注がれた場合、多くは大気を突き抜けて(透過して)地上に達しますが、一部は吸収されたり反射したりします。
一方、砂地に注がれた可視光線は反射したり吸収されたりしますが、透過することはありません。
既に述べたように、物質の中でも黒体は電磁波を完全に吸収します。
3-2. 波長
さらに同じ物質であっても電磁波の波長によって放射特性は変わります。
例えば、太陽放射が大気に達したとき、可視光線はほとんど透過して地表に達しますが、赤外線の多くは大気によって吸収されます。
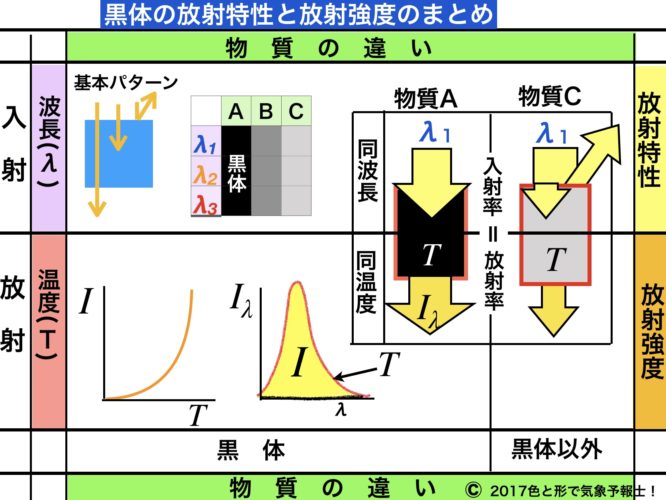
下記の左側の図は以上をまとめたものです(放射強度は後で説明します)。
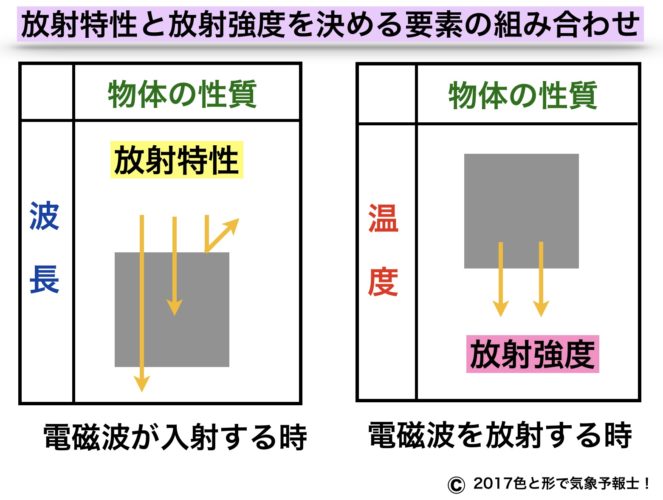
さきほど取り上げた放射特性の2つの要素、物質の性質と波長の組み合わせのイメージを下記の図で示しました。
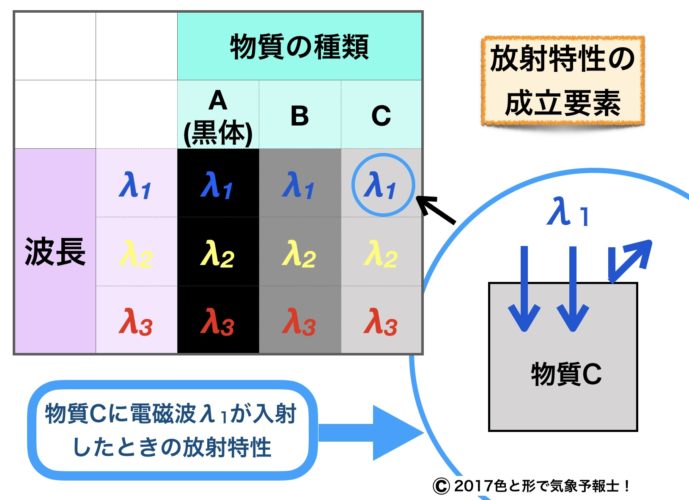
例として物質を3種類挙げました。物質Aは黒体、物質Bと物質Cは黒体ではないとします。また波長も3種類に分けました。
この場合、合計9種類の放射特性を表現できます。
例えば、右上の小さな円で示された部分は物質Cに波長λ1の電磁波が入射した場合を示しています。その部分を拡大して放射特性を表したのが右下の図です。
物質Aは黒体で、λ1、λ2、λ3 を含む全ての波長の電磁波を吸収します。
後述しますが、黒体は全ての波長に関し、吸収率は1となります。
4.放射強度とは
放射に関する言葉の意味をまとめました。
◆ 放射強度
意味・・ある平面の単位面積に単位時間当たり入射する放射エネルギー量
単位・・Wm-2
記号・・I
◆ 単位波長当たりの放射強度
意味・・ある波長領域(λ)における放射強度
単位・・Wm-2μm-1
記号・・Iλ
※ 単位波長当たりの放射強度Iλを全て合計したもの(全放射強度)が 4-1. の放射強度 I になります。
◆ 放射量
放射強度に放射面積をかけた量、と私は解釈しています。不正確だったら修正します。
5.放射強度を決める要素
全ての物体は絶対零度(-273℃)でない限り、その温度に応じた電磁波を放射しています。
放射される電磁波の強さを決めるのは物体の性質と温度の組み合わせです。さきほど挙げた図の右側を参照してください。

5-1. 物体の性質(要素1)
同じ温度でも物質によって放射の強さは変わります。
物体がどれくらいの電磁波を放射するかは、その物体が電磁波をどれくらい吸収するかによります。
この関係を示しているのがキルヒホッフの法則です。
簡単に復習すると、よく吸収する物体ほどよく放射するという法則です。数式にするとこのようになります。ε はイプシロンといいます。
aλ = ελ
aλ : 吸収率 ελ : 放射率
吸収率:物体が吸収したエネルギーと入射してきたエネルギーの比
$吸収率=\frac{\Large{吸収放射量}}{\Large{入射放射量}}$
放射率:物体の単位面積から単位時間に放射されるエネルギーと黒体放射との比
$放射率=\frac{\Large{任意の放射強度}}{\Large{黒体放射強度}}$
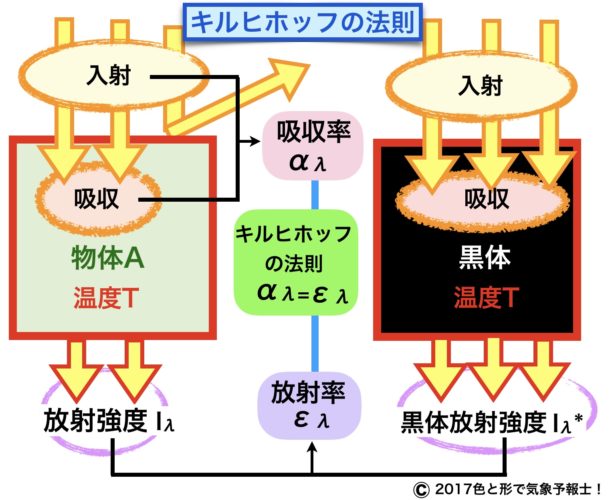
上の図をご覧ください。右側の四角は黒体、左側の四角は黒体以外の物質とします。
それぞれに同じ波長の電磁波が同じ量だけ入射してきたとします。イメージし易いように入射量を矢印3本で表しました。
黒体はどんな波長の電磁波も全て吸収するので矢印3つ分吸収します。
対して黒体以外の物質は全てを吸収するとは限りません。
図のケースだと物体Aに波長λの電磁波が入射したとき、2本は吸収し、1本は反射しています。
すると吸収率とは、吸収量÷入射量 なので
$吸収率\Large α_λ = \frac{2}{3}$
となります。
同様に黒体と物体Aから放射される電磁波も矢印で見てみます。
黒体は温度が同じなら他のどんな物質と比べて最大限のエネルギーを放射します。吸収率が最大だからです。図でいうと矢印3本分放射しています。
それに対し、物体Aは吸収する量が少ない分放射するエネルギーも少なくなります。図では2本分放射となっています。
そして放射率は、放射強度÷黒体放射強度 なので
$放射率\Large ε_λ = \frac{2}{3}$
となり、$ \Large{α_λ = ε_λ}$ が成立します。
黒体の場合、吸収率、放射率とも同じ1になります。
$ \large{α_λ = ε_λ=1}$
5-2. 物体の温度(要素2)
放射強度を決めるもう一つの要素は物体の温度です。
簡単にいえば温度が高いほど放射強度は強くなります。
5-3.ステファン・ボルツマンの法則
物体からの放射についていえば、黒体が関係する幾つかの法則があります。
温度と放射強度の関係を表したのがステファン・ボルツマンの法則(シュテファン・ボルツマンの法則)です。つまり
黒体放射の全ての波長帯のエネルギーの総量I は、黒体の絶対温度T の4乗に比例します。式にするとこうなります。
I = σT4
σ(シグマ)はステファン・ボルツマン定数でその値は下記になります。
σ = 5.67×10-8 Wm-2K-4
特に黒体であることを明確にするため次のように表すことがあります。
I∗= σT4
この法則を感覚的に示したのが下の左側のグラフです。
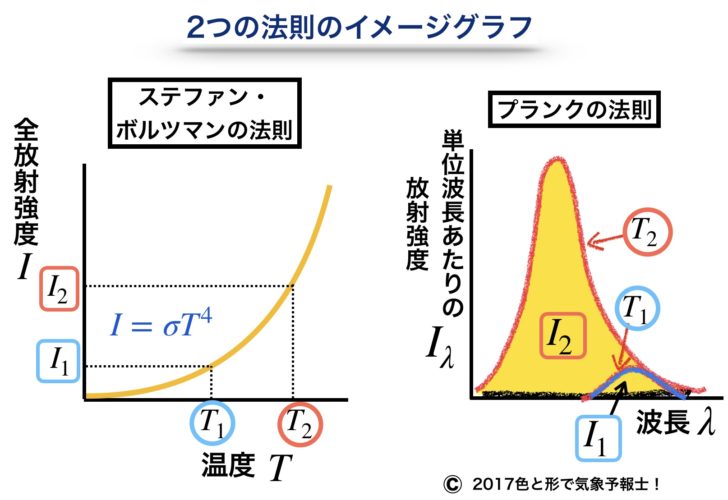
5-4.プランクの法則
ステファン・ボルツマンの法則は全ての波長の放射強度の合計の値ですが、それを波長別に表しているのが、プランクの法則です。
さきほどのイメージ図の右側のグラフをご覧ください。
横軸が波長(λ)、縦軸が単位波長当たりの放射強度(Iλ)を示しています。
Iλ はキルヒホッフの法則の図の黒体放射強度(Iλ∗)と同じものです。
右下の小さい山が低い温度(T1)の波長分布、大きな山が高い温度(T2)の波長分布です。
ここからウィーンの変位則も導き出されます。プランクの法則とウィーンの変位則の意味については「放射に関する法則(放射4)」をご覧ください。
ここまでで黒体と電磁波の関係について考えました。ここでもう一度、まとめとして冒頭のイメージ図を載せます。
次回はこの記事で理解したことを黒体である太陽と地球に当てはめて、放射平衡について考察します。