前回の記事では傾度風を感覚的に捉えましたが、今回は式に当てはめ傾度風の特色を調べていきます。
傾度風は、高気圧や低気圧の周囲、気圧の峰や谷で見られるように等圧線(等高度線)が湾曲している状態で生じます。
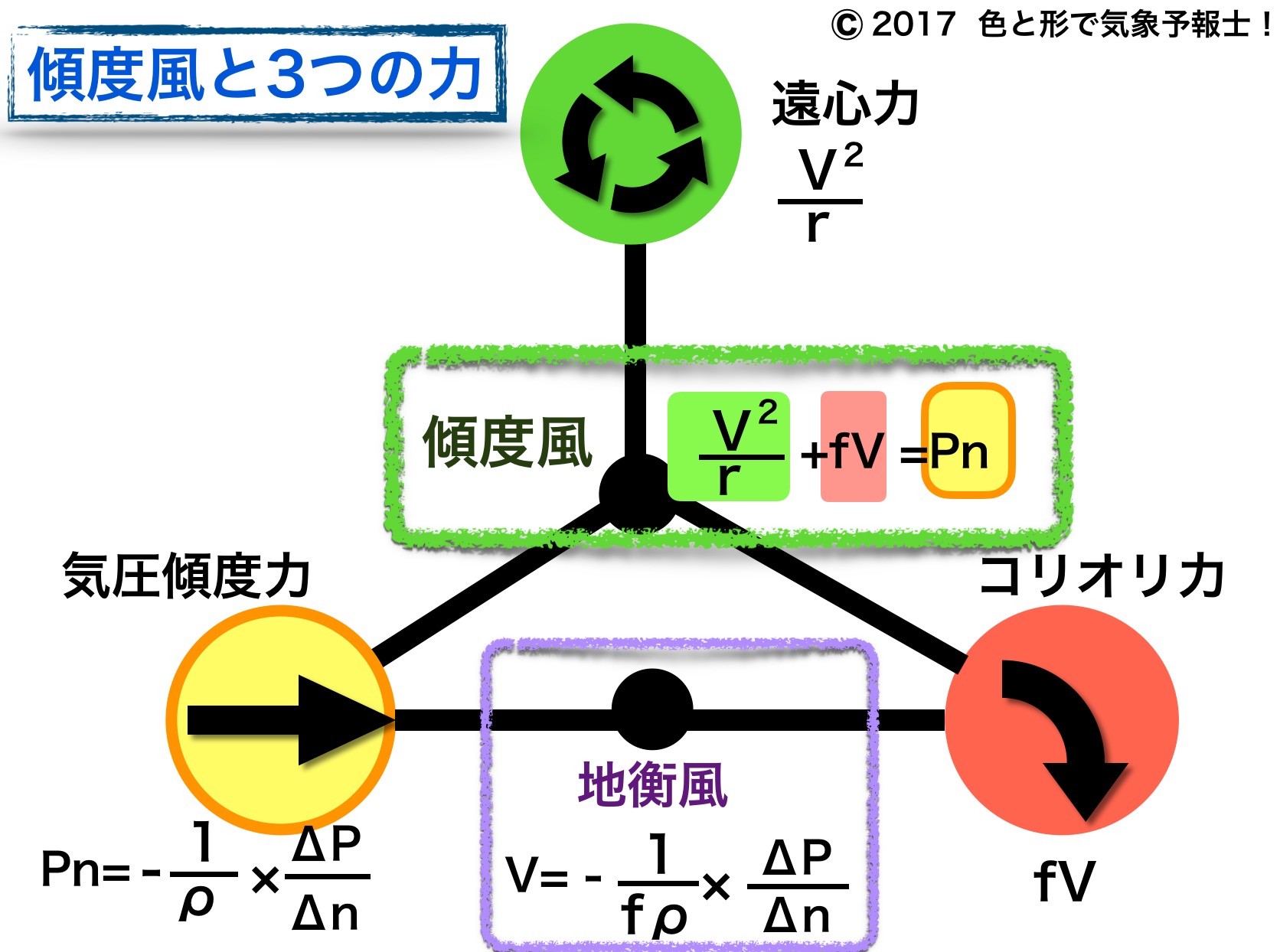
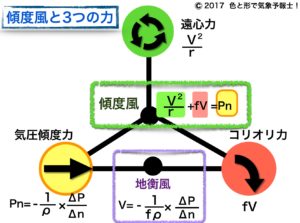
その仕組みは傾度風は気圧傾度力、コリオリ力、遠心力の3つの力のバランスが取れた状態で生じるといえます。
1.傾度風の強さ
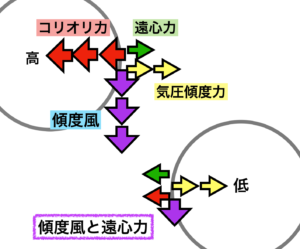
前回の記事「傾度風を感覚的に理解しよう」で使ったイメージ図を基に考えるとこうなります。
● 地衡風平衡・・
コリオリ力=気圧傾度力
● 傾度風平衡(高気圧性循環)・・
コリオリ力=気圧傾度力+遠心力
つまり遠心力の分だけ、コリオリ力が強くなる。
● 傾度風平衡(低気圧性循環)・・
コリオリ力+遠心力=気圧傾度力
変形すると、コリオリ力=気圧傾度力ー遠心力
つまり、遠心力の分だけコリオリ力が弱くなる。
コリオリ力と風の強さは比例するので風の強さはこうなります。
傾度風(高気圧性循環)>地衡風>傾度風(低気圧性循環)
2.傾度風の式
北半球における傾度風の式を考えます。
2-1. 変数の説明
◆ 曲率半径 r
◆ 気圧傾度力 \(Pn=\frac{1}{\rho}\frac{ΔP}{Δn}\)
(気圧が高くなる場合を正とする。)
◆ コリオリ力 fV
(コリオリパラメータ f )
◆ 遠心力 \(\frac{V^{2}}{r}\)
◆ 接線速度(風速) V
(高気圧性循環を負、低気圧性循環を正とする。)
2-2. 低気圧性循環
遠心力+コリオリ力=気圧傾度力 なので
$$\frac{V^{2}}{r}+fV=P_n$$
2-3. 高気圧性循環
遠心力+気圧傾度力=コリオリ力 なので
$$\frac{V^{2}}{r}+P_n=fV$$
2-4. まとめると
傾度風は高気圧性循環と低気圧性循環とでは、風の強さだけでなく向きも異なります。
そこで、低気圧性循環の方の式に統一します。また、
$$気圧傾度力 P_n=\frac{1}{\rho}\frac{ΔP}{Δn}$$
なので、まとめると次の式になります。
そして、高気圧性・低気圧性の気圧変化や運動の向きの違いを考慮して次の通り区別します。
低気圧性循環 ΔP>0、V>0
高気圧性循環 ΔP<0、V<0
上記の式から 傾度風V を導き出すことができます。
3.地衡風平衡+遠心力
冒頭にもあったイメージ図から説明します。
◎ 地衡風平衡
気圧傾度力=コリオリ力
Pn = fV
◎ 傾度風平衡
地衡風平衡+遠心力
低気圧性循環の式を用いるので
$$\frac{V^{2}}{r}+fV=\frac{1}{\rho}\frac{ΔP}{Δn}$$
となります。
4.傾度力の式の覚え方
こちらの記事をご覧ください。
「傾度風・地衡風・気圧傾度力の式とコリオリパラメータを一気に覚えちゃおう」
次は旋衡風(竜巻)を調べます。