今回はコリオリ力の向きと大きさ、特にコリオリ力の求め方について調べていきます。
文系初心者にとっては、見たことのない記号が出て来る式はスルーしたいというのが本音ですが、そうもいかず。。 でも過度に深深入りしなければ言ってることはそう難しくもありません(多分)。
1.コリオリ力(転向力)の向き

これまでの記事でも少し触れましたが、北半球と南半球とでは向きが逆になります。
図にあるように北半球では物体の運動方向の直角右向きに働きます。
このため物体の進行は右へ右へと曲げられます。
南半球では反対に物体の運動方向の直角左向きに働き、物体の進行は左へ左へと曲げられます。
2.回転効果
コリオリ力は地球の回転(自転)効果を表す見かけ上の力です。
ですから、コリオリ力の大きさは回転効果の大きさと言うことができます。
そして、コリオリ力の大きさは地球上どこでも同じということではありません。
高緯度ほど大きくなり、北極・南極で最大となり赤道では0です。
他にもコリオリ力の大きさを決める要素があります。これから、それらの要素に注目しながらコリオリ力の大きさを求める方法を探って行きます。
3.コリオリ力の大きさを決める要素
地球に限定すると要素は次の3つになります。
【質量】【物体の速度】【緯度】
そして、コリオリ力は
❶ 質量が大きいほど
❷ 物体の速度が速いほど
❸ 緯度が高いほど
大きくなります。それで、これら3つの要素を基準に大きさを求めます。
4.コリオリ力の求め方
イメージ図も見ながら順に考えます。
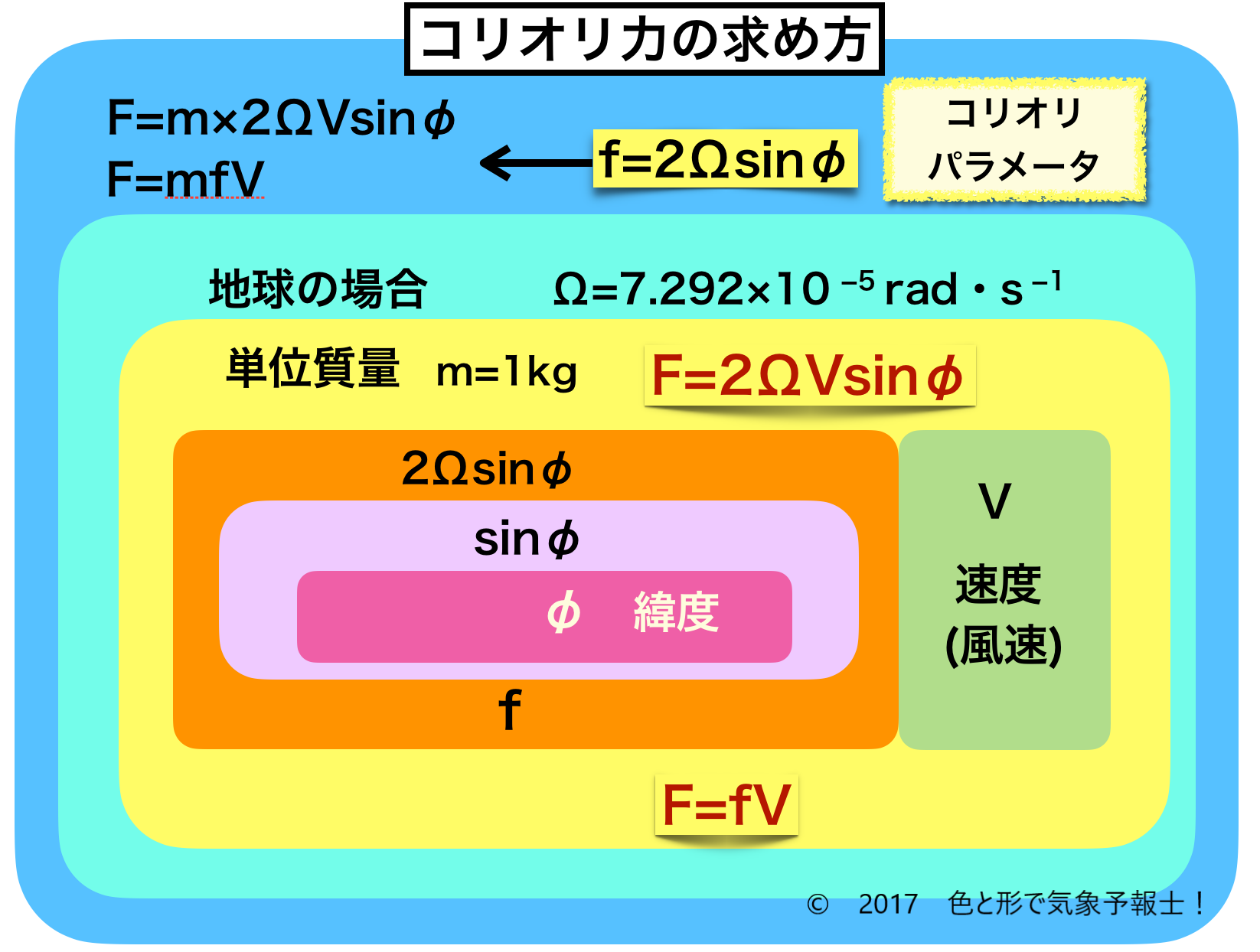
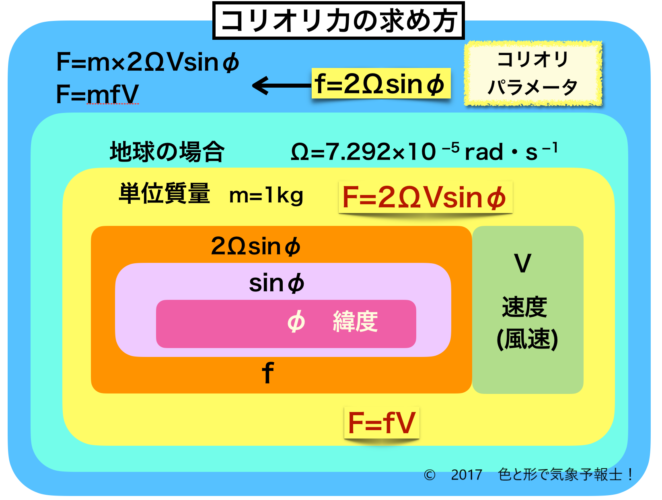
4-1. 求め方の式(図の外側の青いところ)
3つの要素を含んだ式はこうなります。
F = m×2ΩVsinΦ ・・(1)
F : コリオリ力
m:質量[kg]
Ω:角速度[rad·s-1]または[s-1]
V:物体の速度[ms-1]
sin:三角関数の1つ(※)
Φ:緯度
● 2ΩVsinΦ の読み方は「2オメガ ヴイ サイン ファイ」です。rad は「ラジアン」です。
● 角速度とは回転速度の表現のひとつで、1秒間にどれくらい回転したかを表した数値のことです。単位は rad·s-1 と s-1 どちらも使います。
4-2. コリオリパラメータ
上記の式のうち、質量と物体の速度以外の値は緯度によって決まります。そこで、
f = 2ΩsinΦ ・・(2)
とし、これをコリオリパラメータ(コリオリ因子)と呼びます。
コリオリパラメータは惑星渦度とも呼ばれます。
(1)の式に(2)を代入すると こうなります。
F = mVf ・・(3)
4-3. 地球の気象現象に当てはめると(図の緑色のところ)
(1)の式がこう絞られます。
m:(主に)空気塊の質量
V:(主に)風速
Ω:自転の角速度の値 7.292×10-5rad·s-1
4-4. 単位質量を用いると(図の黄色いところ)
m=1kg とし、これを単位質量とすると(1)、(3)の式はそれぞれ
F = 2ΩVsinΦ ・・(4)
F = fV ・・(5)
となります。この時
F は質量 1kg にかかる力であり、その単位は Nkg-1 です。
N(ニュートン)は力の単位です。詳しいことは「気象学における物理量と単位(2)」をご覧ください。
上記の2つの式が最もよく使われています。
※ コリオリパラメータの覚え方は「傾度風・地衡風・気圧傾度力の式とコリオリパラメータを一気に覚えちゃおう」に載せています。
5.比例関係
以下が比例関係にあります。
F = mVf の式から
◆ コリオリ力F と質量m
◆ コリオリ力F と物体の速度V
◆ コリオリ力F とコリオリパラメータ f
F = m×2ΩVsinΦ の式から
◆ コリオリ力F とsinΦ (コリオリパラメータのうち、2Ωの値は一定なので)
以上のことから、単位質量あたりで考えた場合、
風速が一定の場合、コリオリ力は緯度で決まり、
緯度が一定の場合、コリオリ力は風速で決まる
ということができます。
6.緯度ごとのコリオリ力の大きさ
F = 2ΩVsinΦ の式のΦにそれぞれの緯度の数値を当てはめます。
◎ 赤道上 緯度0度なので
F = 2ΩVsin0° sin0°=0
F = 2ΩV×0
F=0
赤道上ではコリオリ力は働かないことが分かります。
◎ 北緯30度
F = 2ΩVsin30° sin30°=0.5
F = 2ΩV×0.5
F = ΩV
◎ 北極 北緯90度なので
F = 2ΩVsin90° sin90°=1
F = 2ΩV×1
F = 2ΩV
北極と南極ではコリオリ力が最大になります。
コリオリ力を求める式は、これからも使われるのでしっかり覚えておきたいですね。
(※)三角関数については「気象予報士かんたん合格テキスト 学科一般知識編(技術評論社)」の付録「数学・物理の基礎」で分かり易く解説されています。
7.まとめ
▶ コリオリ力の向き
北半球:右 南半球:左
▶ コリオリ力は
● 質量が大きいほど
● 速度が速いほど
● 緯度が高いほど 大きくなる
▶ コリオリ力F の式
F = 2ΩVsinΦ または
F = fV
(コリオリパラメータ f = 2ΩsinΦ)
▶ 緯度別コリオリ力
● 赤道上 F=0
● 北緯30度 F = ΩV
● 北極 F = 2ΩV