スカイツリーの展望台で窓を開け(開かないでしょうが)、空気の塊に赤い色をつけて離したらどうなるでしょうか?(頭の中の実験です。)
空気にも質量があるので重力で赤い空気は地上に落ちてくるはずです。でも、実際には落ちてこないでしょう。
逆に上空に上って行くと考えられないでしょうか?上空ほど気圧は低く、空気は気圧の高い方から低い方へ移動するからです。でも、実際には上昇もしないでしょう。
今回はこの謎(?)を解いていきます。
目次
1.静力学平衡(静水圧平衡)とは
上昇気流や下降気流がなければ、空気は上にも下にも行かないはずです。それは空気に働く重力と、空気の上下の圧力の差が釣り合っているからです。
このように鉛直方向に運動がなく、釣り合って平衡している状態のことを静力学平衡(静水圧平衡)の状態といいます。
このつり合った状態について空気分子の鉛直方向の分布から説明された次の記事も参考にしてください。「空気は流体」の 6-2.
※ 静力学平衡と層厚については、「熱力学」と「大気の力学と運動」、両方の分野で取り上げられる場合が多いようです。
2.高さの差と気圧の差
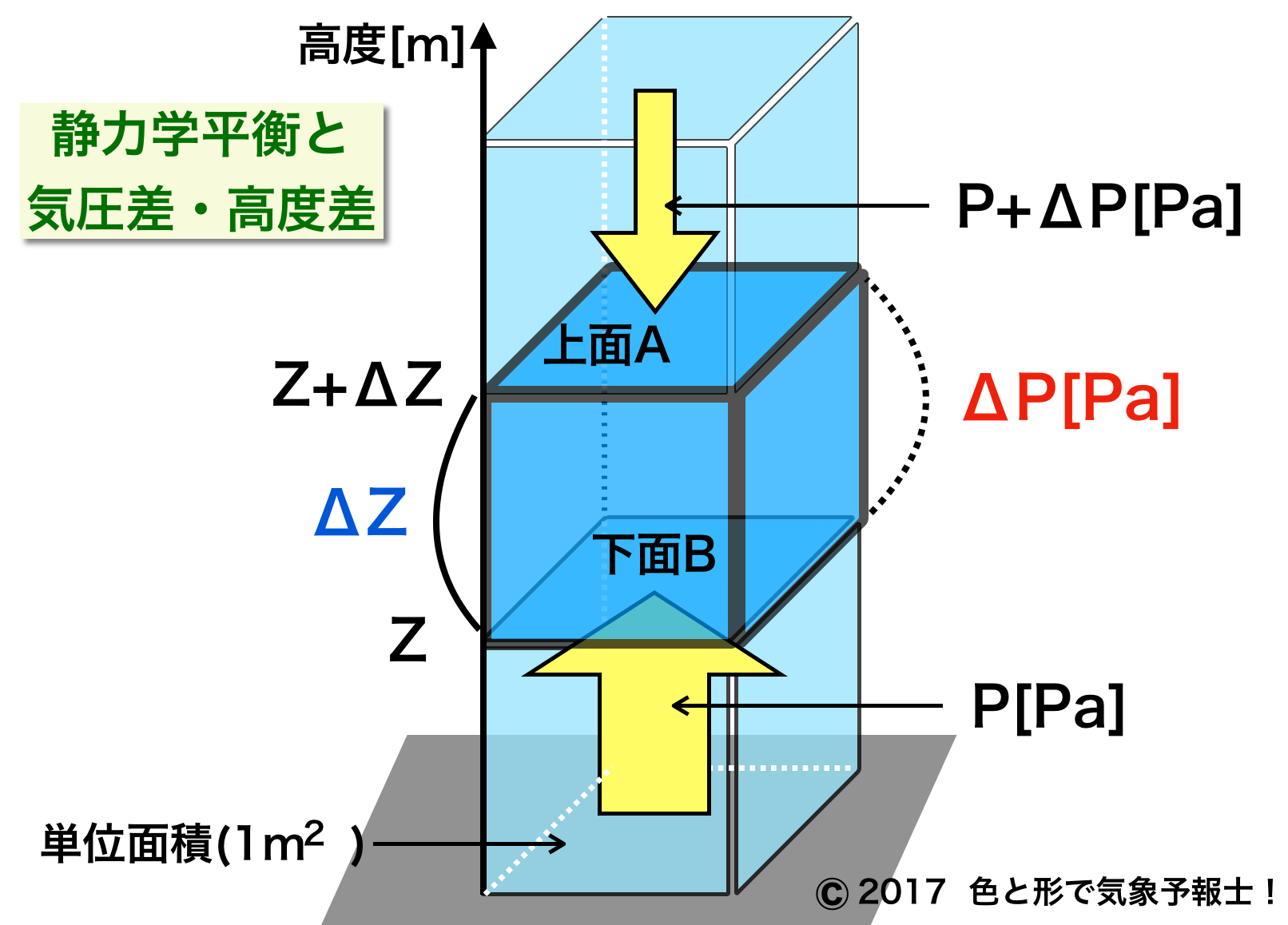
静力学平衡がどのように生じるかを一つの気柱をモデルに考えてみます。
図の濃い青い部分の直方体を一つの気塊とみなします。
この直方体は単位面積を 1m2 とする地表面の上空にあるとします。
下面Bの高度をZ、上面Aの高度をZ+ΔZとすると、この直方体の高度の差は ΔZ になります。
次に下面Bに働く圧力をP、上面Aに働く圧力をP+ΔPとすると、直方体にかかる圧力の差はΔPになります。
3.気圧傾度力と重力
ここでもう一度、静力学平衡の意味を確かめます。
力という点で見ると、静力学平衡とは下向きに働く重力と上向きに働く気圧傾度力がつり合った状態といえます。力の向きを考慮せず、大きさだけで比べるなら
気圧傾度力=重力
というわけです。ただ、力の向きが逆なので重力にマイナスを付けると
気圧傾度力=-重力
になります。では、図に示したように高度の差がΔZ、気圧の差がΔP だとすると気圧傾度力と重力の大きさは、それぞれどのように導き出せるでしょうか?
4.気圧傾度力の式
水平方向の気圧傾度力については「大気の力学と運動」のジャンルの「気圧傾度力 風が吹くのはなぜ?」の記事で詳しく扱っています。その時載せた図がこれです。ちょっと復習します。
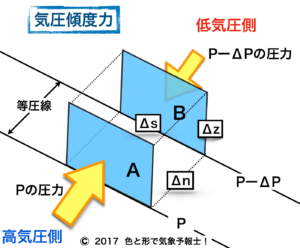
● 高気圧側の面をAとし、低気圧側の面をBとする
● A,Bの面積は Δs×Δz
● A,B間の距離は Δn
● Aにかかる圧力は圧力は P
● Bにかかる圧力は P–ΔP
● 両者の差は ΔP
● 直方体(気塊)の密度を ρ (ロー)とする
こうすると気圧傾度力の式はこうなります。
$$気圧傾度力 Pn=–\frac{1}{\rho}\frac{ΔP}{Δn}$$
この場合の気圧傾度力は水平方向のものです。これを今 考慮している鉛直方向の気圧傾度力に直すため、少々変換します。
● 高気圧側の面Aを低い高度の下面Bとする
● 低気圧側の面Bを高い高度の上面Aとする
● 距離の差 Δn を高さの差 Δz とする
こうすると気圧傾度力の式はこうなります。
$$気圧傾度力=–\frac{1}{\rho}\frac{ΔP}{Δz}$$
5.重力の式
では、空気塊を表す直方体の重力はどのようにして求められるでしょうか?
◆ 重力=質量×重力加速度
◆ 質量=密度×体積
◆ 体積=単位面積×高さの差
(今回は直方体の底面を単位面積としているので、体積は高さの差によって計算できます。)
以上まとめて、重力加速度:g、密度:ρ、高さの差:Δz とすると
重力=gρΔz となります。
6.気圧傾度力=-重力(?)
さて、前述したように静力学平衡の基本は上記の式です。
ここで、これまで考えたように気圧傾度力の式、重力の式、それぞれを当てはめるとこうなります。
\(–\frac{1}{\rho}\frac{ΔP}{Δz}=g\rhoΔz\)
なんか変ではないでしょうか? ΔP= に直すと
ΔP=–gρ2Δz2 になってしまいます。
冒頭の図にあったように静力学平衡の式は
ΔP=–gρΔz です。この違いの理由は次のイメージ図を使うと分かります。
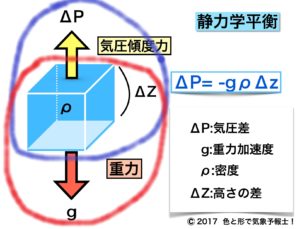
紫色で囲まれた部分が
$$気圧傾度力=–\frac{1}{\rho}\frac{ΔP}{Δz}$$
を示しています。
一方赤で囲まれた部分は
重力=gρΔz
を示しています。
ぱっと見て分かるように直方体の部分が重なっています。
両方の式にこの部分が含まれてしまっているので、式がおかしくなってしまいます。
それで、直方体はどちらか一方の式に含めるようにすると次の2つの式が成り立ちます。
■ \(–\frac{1}{\rho}\frac{ΔP}{Δz}=g\)
■ ΔP=–ρgΔz
大概は下の式が用いられるようです。
▷ この記事の終わりに静力学平衡の式の覚え方(イラスト)を載せました。
7.気象において静力学平衡が持つ意味とは
気象現象の多くは静力学平衡が当てはまります。つまり、大気は上にも下にも行かないということです。
これって変ではないでしょうか?低気圧や高気圧について学ぶときには、散々上昇気流だとか下降気流だとかが天気を左右するって聞いてきました。
これを理解するには大気の運動スケールを考慮に入れる必要があります。
大部分の気象現象は対流圏において生じます。その対流圏の厚さは6~16km程度ですから、気象現象の鉛直方向のスケールもその範囲に収まります。
それに対し、気象現象の水平方向のスケールは何千kmにも及びます。
例えば、高気圧や低気圧の鉛直スケールは10km程度ですが、水平スケールは2000km以上にもなります。
高気圧・低気圧における大気の運動速度についても、鉛直方向は数cm/s、水平方向には数m/s程度で、2桁の違いがあります。
低気圧や高気圧のような水平スケールが2000km以上になる現象を総観規模擾乱といいます。
主に総観規模以上の擾乱を解析する全球モデル(GSM)という数値予報システムでは、静力学平衡が成り立つという前提(静力学近似という)で様々な方程式を用いて計算し、予測を行っています。
8.静力学平衡が成り立たないケース
ただし、水平スケールの小さな気象現象では静力学平衡が成り立ちません。
例えば1つの積乱雲のスケールを考えると、水平方向のスケールは数km、鉛直方向のスケールは5~10km程度ですから、水平方向と鉛直方向の運動スケールが同程度になります。
また積乱雲内では数m/s 以上の強い上昇気流や下降気流が存在し、鉛直方向の運動も活発です。
このような擾乱では、鉛直方向の運動も考慮した非静力学モデルも運用されて精度の良い予報ができるようになっています。
9.まとめ
▶ 静力学平衡・・鉛直方向に運動がなく、釣り合って平衡している状態
気圧傾度力=-重力
▶ $気圧傾度力=–\frac{1}{\rho}\frac{ΔP}{Δz}$
▶ 重力=gρΔz
▶ ΔP=–ρgΔz
10.静力学平衡の式の覚え方
▷ 静力学平衡の式の覚え方のイラストです。
頭に三角のPを乗せたお爺さんが宙を浮いているイメージです。
覚え方は・・
デルP(ΔP)は(=)My(マイナス)老(ρ)人(g)デルターZ(ΔZ)
てな具合です。
次回は静力学平衡の応用として、海面更正と層厚について取り上げます。