天気予報に欠かせないもの、晴れか雨か、暑いか寒いか、そして風が強いか弱いか・・
ここでは風を吹かせる力、気圧傾度力について考えます。
1.風とは
風とは何か?それは動いている空気です。
もうちょっと固い言い方をすると、風とは
「水平方向の空気の流れ」「空気分子が一定の方向に一斉に動く現象」
となります。
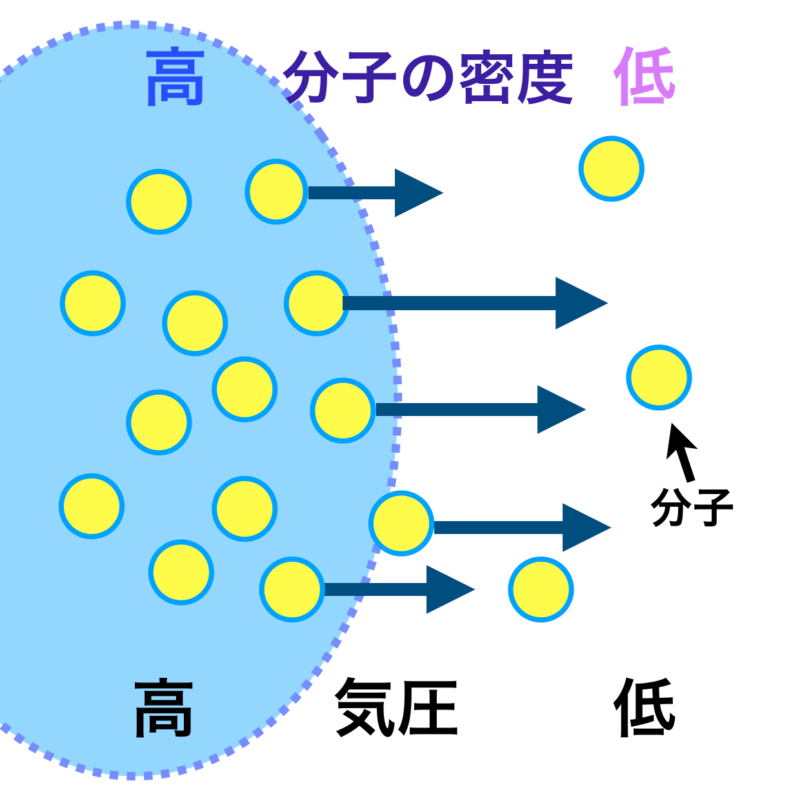
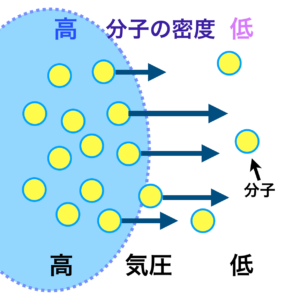
イメージ図にあるように大気には、空気分子の密度の高い領域と低い領域があるとします。
密度の高いところは気圧が高く、低いところは気圧が低いと言い換えることができます。
このとき気体のように流動性のある物質では密度を均一化しようして、つまり同じ気圧にしようとして空気分子の移動が始まり、これが風の発生となるわけです。
風は空気が水平方向に移動するのに対して、垂直方向に移動するのには「気流」という言葉を使います(上昇気流など)。
2.気圧傾度とは
何かを動かすには力が必要です。空気を動かす力が気圧傾度力です。
気圧傾度力は気圧傾度がある場で生じます。
高気圧など気圧の高い場所と低気圧など気圧の低い場所の間には気圧差があります。このとき気圧傾度が生じるといいます。
イメージとしては山と谷との間の斜面が思い浮かびますね。
他の資料ではこう定義されています。
「気圧傾度とは気圧の空間変化率のことです。」(気象予報士かんたん合格テキスト 一般知識編)
「距離に対する気圧の変化の割合。ベクトルで表され,大きさと方向をもつ。通常はその水平成分をさす。気圧傾度の向きは高気圧から低気圧への方向を正とする。天気図上では,等圧線の密集している気圧傾度の大きいところで風が強い。」(ブリタニカ国際大百科事典 小項目事典の解説)
気圧傾度には水平気圧傾度と鉛直気圧傾度があります。これから取り上げるのは全て水平気圧傾度です。
鉛直気圧傾度は静力学の式で表されますが、別の記事で取り上げる予定です。
3.水平方向の気圧傾度の求め方
気圧傾度の求め方は次の通りです。
例えば、A地点の気圧が1000hPa、B地点の気圧が970hPa 、AB間の距離が300km のときの気圧傾度は次のように求めます。
$$気圧傾度=\frac{ΔP}{Δn}=\frac{30hPa}{300km}=0.1hPa/km$$
4.気圧傾度の次元解析
次元解析については「気象学における物理量と単位(2)」も参照してください。
※ 次元解析まで説明しているテキストは多くないので、そこまで調べなくていいという方は飛ばしてください。
気圧傾度の単位[hPa/km] を kg(質量)、s(時間)、m(距離)の単位に直して表現(次元解析)します。
1hPa = 100Pa
圧力(Pa)=力(N)/面積[m2] なので
1Pa=1N/m2
力(N)=質量[kg]×加速度
加速度=速度/時間[s]
速度=距離[m]/時間[s]
1Pa= 1kg・m・s-2 / m2
= 1kg・m-1・s-2
1hPa/km = 100Pa/km
= 100[kg・m-1・s-2]/1000[m]
= 10-1kg・m-2・s-2
まとめると下記になります。
気圧傾度の単位: 10-1kg・m-2・s-2
5.気圧傾度力とは
気圧傾度力とは、気圧傾度によって発生する、空気塊に働く力の大きさを意味します。
簡単にいえば、気圧の高い方から低い方へ空気を押す力のことです。
6.気圧傾度力の求め方
図を使って説明します。
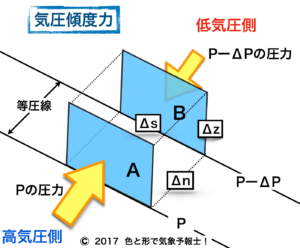
この図は小さな空気の直方体空間を示しています。気塊と考えてもいいと思います。
2本の線は等圧線です。
面A側(手前)の等圧線は気圧 P の線です。
面B側(向こう側)の等圧線との間には気圧差 ΔP があるとすると、面B側の等圧線は気圧 P-ΔP の線になります。
例えば面A側が1000hPa、面B側が970hPa、気圧差が30hPa といった具合です。
では、面Aに働く圧力はどう表せるでしょうか?
面は2次元なので図でいうとΔs×Δzの値が面積となります。
その面積に気圧Pが押すわけですから、面Aに働く圧力は、
–PΔsΔz
です。ここで符号がマイナスになっているのは圧力の働く向きを示すためです。
気圧傾度力がどれだけ気圧の低下する方向に働くのか、という意味があります。
同じように考えると面Bに働く圧力は次のようになります。
(P–ΔP)ΔsΔz
そして面Aに働く圧力と面Bに働く圧力の差が、この空間に働く圧力ということになります。つまり
ΔPΔsΔz となります。
圧力は本来、面(2次元)に働く力として表されています。
でも気塊のような空間(3次元)には体積があります。ですから気圧傾度力は体積のあるものに働く力と考えなければなりません。
さらに体積がバラバラでは力の大きさを比べることはできません。
それで上記の圧力ΔPΔsΔzを体積 ΔsΔzΔn で割って単位体積あたりの力を割り出します。
すると、次の式で分かるように、面積部分は分母・分子両方にあるので、残った距離だけが分母になります。
$$\frac{ΔPΔsΔz}{ΔsΔzΔn}=\frac{ΔP}{Δn}$$
さらに高気圧から低気圧の方向へ直角に働くのでマイナスの符号を付けます。
$$–\frac{ΔP}{Δn}$$
また、体積が一緒でも空気の密度が違えば質量が違ってきます。力は 質量×加速度 ですから、質量がバラバラでは力の大きさを比べることはできません。
それで、上記の式を質量で割って単位質量あたりの力を求めます。
密度は 質量/単位体積 ですから、密度の逆数、つまり 単位体積(=1)/質量 をかければ質量で割ったことになります。
密度を ρ とすると式は次の通りになります。
$$−\frac{1}{\rho}\frac{ΔP}{Δn}$$
まとめると、こうなります。
7.気圧傾度力の次元解析
ここからは私自身十分理解しきれないところがあるので参考程度にしておいてください。
気圧傾度力 Pn=\(–\frac{1}{\rho}\frac{ΔP}{Δn}\) を
\(-\frac{1}{\rho}\) と \(\frac{ΔP}{Δn}\) に分けてみます。
密度ρ の単位は[kg/m3] なので、密度ρ の逆数の単位は[m3/kg] つまり[m3kg-1] となります。
また、\(\frac{ΔP}{Δn}\) は気圧傾度と同じですから、単位は
10-1kg・m-2・s-2 です。2つの単位を合わせると
m3kg-1 × 10-1kg・m-2・s-2 = 10-1ms-2 となります。ですから
気圧傾度力 Pn=\(–\frac{1}{\rho}\frac{ΔP}{Δn}\)[ms-2]
となります。そして、この単位 [ms-2] は加速度の単位でもあります。
気圧傾度力は大気の力学と運動を理解する要となるものです。
次回はもう一つの要であるコリオリの力について調べます。