天気予報は発表して「はい、終わり」ではありません。
予報がどれくらい当たったかを後で集計して、その精度を評価します。
これを予報精度評価、あるいは天気予報の評価といいます。
1.評価による予報の分類
天気予報は短期・中期・長期といった予報の期間による分類があることを既に学びました。
これとは別に、精度を評価する方法による分類もあります。それが以下の3種類です。
▶ カテゴリー予報
▶ 確率予報
▶ 量的予報
これから、3種の予報ごとに予報精度評価の方法を調べていきます。今回はカテゴリー予報の前半です。
2.カテゴリー予報
カテゴリー予報とは、ある現象があるかないかを予報して、実際にその現象があったかないかを調べて評価する予報です。
現象をある・なしについてのカテゴリー(範囲)に振り分けることからカテゴリー予報という名が付けられています。
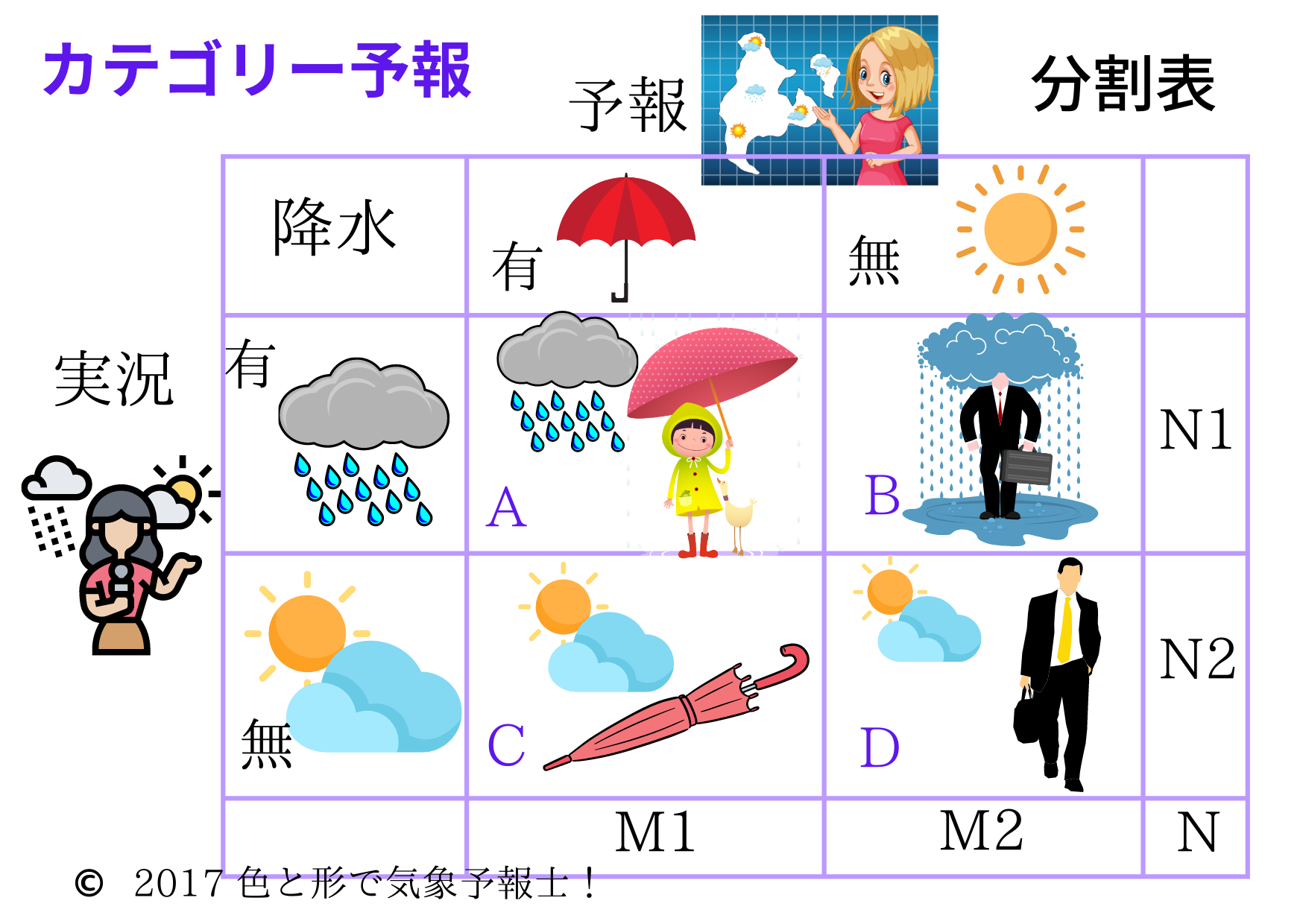
具体的には下の図表にあるような分割表を作って評価します(イメージしやすいようにイラスト入りにしました)。
ここでは降雨のありなしで説明します。
表の上に「予報」とあります。その下の有(傘マーク)は雨が降るという予報をしたことを示しています。
右隣の無(太陽マーク)は雨が降らないという予報です。
表の左に「実況」とありますね。上の有(雨マーク)は実際に雨が降ったことを示しています。
下の無(太陽と雲)は雨が降らなかったことを示しています。
次に表の中のアルファベットの意味を説明します。なお、どんなアルファベットや記号を使うかに決まりはありません。
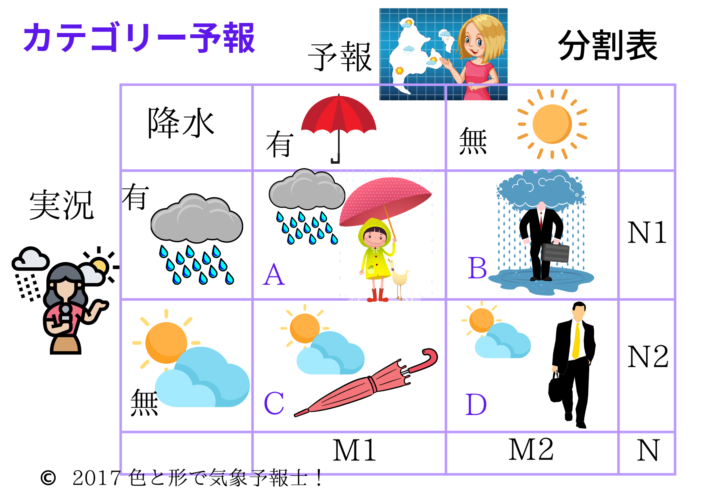
この分割表ではA、B、C、D とあります。意味は次のようになります。
A:雨の予報で実際に雨が降った回数 ⇒ 気象予報士が感謝される
B:雨は降らない予報だったのに実際には降った回数 ⇒ 気象予報士が恨まれる
C:雨の予報だったけど実際には降らなかった回数 ⇒ 傘が邪魔
D:雨が降らない予報で実際に降らなかった回数 ⇒ 天気予報見たことなど覚えちゃいない。
さらに、外側の記号の意味はこうなります。
M1:雨予報の合計(A+C)
M2:雨なし予報の合計(B+D)
N1:雨が降った回数の合計(A+B)
N2:雨が降らなかった回数の合計(C+D)
N:全ての予報回数の合計(A+B+C+D)
では、さっそく分割表をもとに計算方法を見てみましょう。以下も降雨を例にして説明します。
下の図表をご覧ください。
3.適中率
適中率は予報が当たった割合です。
雨予報で雨だった回数(A)と雨なし予報で雨が降らなかった回数(D)の合計を予報の総数(N)で割った値になります。計算式はこうなります。
$\dfrac{A+D}{A+B+C+D}$ または $\dfrac{A+D}{N}$
図のグラフにあるように、数値が高いほど精度が高い、つまり当たっていることになり、予報全てが当たると値は1、全てはずすと0になります。
このようにして求める適中率は春や秋などいろんな天気が偏りなく起きる場合に適しています。
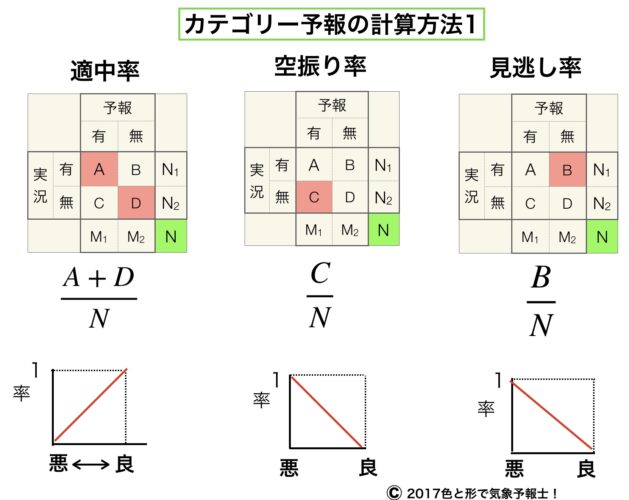
4.空振り率
空振りというのはある現象が起きると予想したのに、実際には起こらなかったことを意味しています。計算方法は以下になります。
$\dfrac{C}{A+B+C+D}$ または $\dfrac{C}{N}$
グラフにあるように、数値が大きいほど精度が悪いです。予報を外したわけですからね。
5.見逃し率
見逃しとはある現象が起きないと予報したのに、実際には起きてしまったということです。計算式は以下になります。
$\dfrac{B}{A+B+C+D}$ または $\dfrac{B}{N}$
見逃し率も数値が大きいほど精度は悪いといえます。こちらもハズレですから。
6.バイアススコア
バイアススコアとは、実況の合計回数に対する予報の合計回数の比を表したものです。
降雨についていえば分母を実際に雨が降った回数、分子を雨予報の回数として計算します。
次の図表をご覧ください。
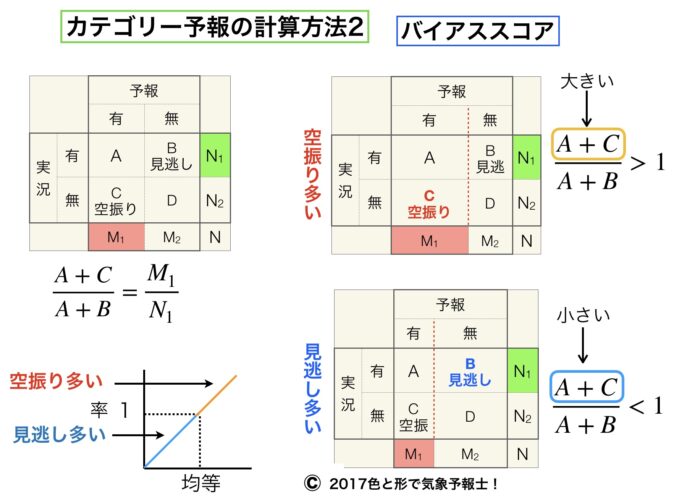
計算式は以下になります。
$\dfrac{A+C}{A+B}$ または $\dfrac{M_1}{N_1}$
バイアススコアの値によって、その予報が空振りが多いのか見逃しが多いのかを判断できます。
◆ 1より大きい <空振りが多い>
実際に起きた回数に対して起きると予報した回数の方が多い
1より大きくなるほど空振り率が大きくなります。
◆ 1 <均等>
実際に起きた回数と起きると予報した回数が同じ
◆ 1より小さい <見逃しが多い>
実際に起きた回数に対して起きると予報した回数の方が少ない
1より小さくなるほど見逃し率が大きくなります。
このようにバイアススコアによって空振りと見逃しのバランスを知ることができます。
7.スレットスコア
スレットスコアは発生することの少ない現象の適中率を評価する方法です。
次の図表をご覧ください。塔は東京タワーのつもりです。
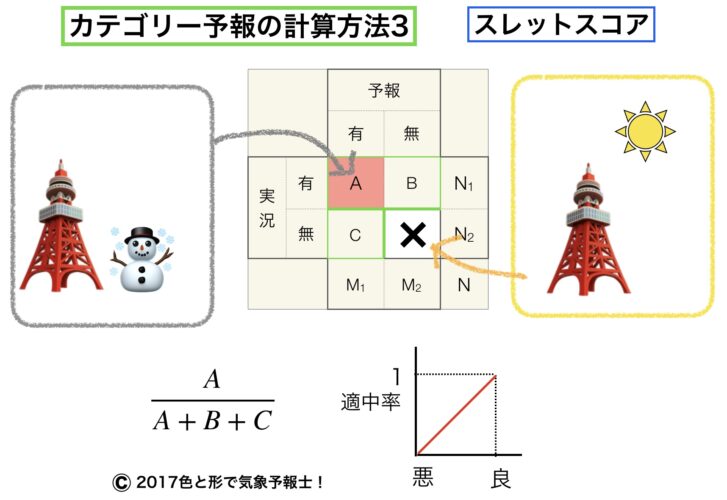
例えば真冬に太平洋側で雪が降る・降らないの予報を出す場合を考えてみます。
西高東低冬型の気圧配置の時、太平洋側、例えば東京地方で雪が降ることは非常に少ないです。
今日も明日も明後日も雪が降らない予報をしていればほとんど当たり適中率は非常に高くなります(右のイラスト)。
でも、こんな適中率はあまり意味がありません。
こういう場合、意味ある適中率は、雪が降るという予報を出して当たった(左のイラスト)または外れた、雪が降る予報を出していなかったのに雪が降ってしまった、以上を分母にして割り出したものです。
それで、もともとのカテゴリー表のD(雪が降らない予報で実際に雪が降らなかった回数)を予報回数としてカウントしないことにします(Dを消して×にしてます)。
ですから計算式は以下になります。
$\dfrac{A}{A+B+C}$
以上がカテゴリー予報の基本です。
カテゴリー予報は警報・注意報の精度を評価するのにも用いられます。次回、取り上げますね。