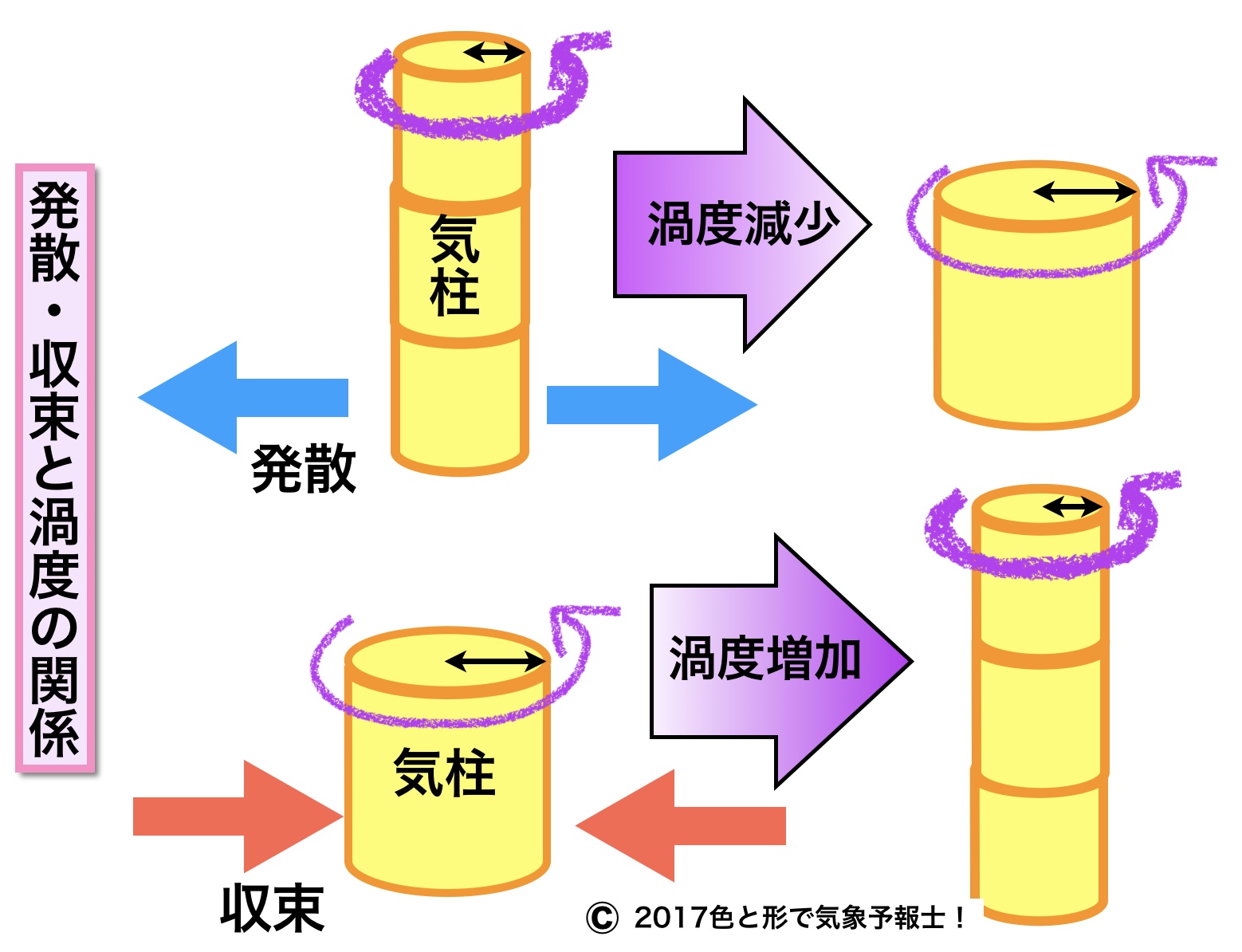
発散・収束は渦度に影響を及ぼします。渦度の解析を500hPa面でするのは、その高さでは発散や収束による渦度の影響が少ないからです。
前回の記事「発散・収束の関係、加えて発散・収束・渦度の種類をまとめました」では発散と収束の関係を調べました。今回は発散・収束と渦度にどんな関係があるのか調べてみます。
1.発散・収束と物体の背の高さの関係
冒頭の図をご覧ください。一つの円筒形の物体(ここでは気柱)を想定します。この気柱について空気の発散・収束があるとどうなるでしょう?
◎ 収束する場合(下)
この気柱に周囲から空気が収束してくるとします。すると気柱の高さが高くなります。
ちょうど、ろくろ台の上で回っている粘土を手で横から押すと、粘土は上に伸びるようなものです。
この時、粘土は細くなります。つまり半径が小さくなります。
◎ 発散する場合(上)
逆に気柱から空気が周囲に発散すると気柱の高さは低くなります。そして気柱の半径は大きくなります。
2.角運動量保存則
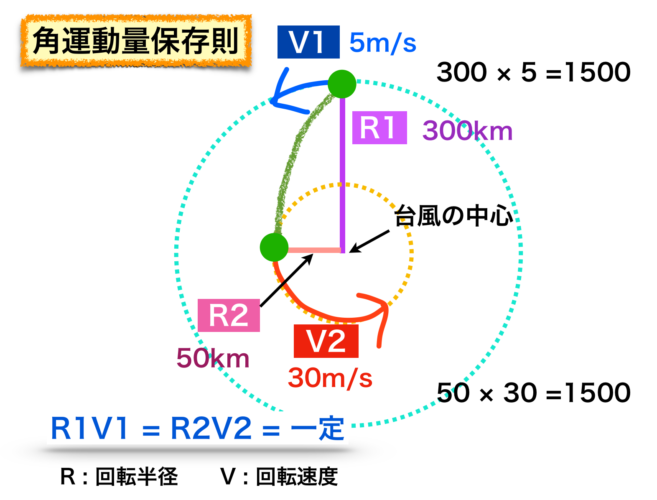
次に半径と風速の関係を考えます。以前、台風についての記事「中心付近で風速が最大」で角運動量保存則を紹介しました。その時のイメージ図を載せます。
角運動量保存則を分かりやすく言えば次の通りです。
「回転する物体の回転半径と回転速度をかけた数値は一定に保たれる」
R1 × V1 = R2 × V2 = 一定
(R:回転半径 V:回転速度)
円筒形の気柱に当てはめるなら半径が小さくなると風速は大きくなり、半径が大きくなると風速が小さくなるということです。
3.発散・収束と渦度の関係
渦度とは大気の回転方向と速さを表す物理量です。
ですから、風速が大きくなると渦度も大きくなり、風速が小さくなると渦度も小さくなります。これまでの流れをまとめると次のようになります。
▷ 発散⇒渦度減少
▷ 収束⇒渦度増加
▷ 発散・収束なし⇒渦度変化なし
▷ 500hPa面(非発散面)⇒渦度解析
渦度はこの先もあちらこちらに出没するようなので、基本を忘れないでいたいですね。