今回は熱力学の第一法則を基に 定圧変化・定圧比熱、定積変化・定積比熱を調べます。まずは熱力学の第一法則の復習から
目次
1.熱力学の第一法則の復習
ΔQ=ΔU+ΔW (1)
Δ:変化量
Q:気体に加える熱量
U:気体の内部エネルギー
W:仕事に使われるエネルギー量
※ この場合の仕事とは:気体が外部にする仕事
具体的には空気塊が周りの空気を押しのけて膨張するということ
2.定圧変化と定圧比熱
2-1. 定圧変化とは
定圧変化とは圧力を一定とした状態変化のことです。
風船のような柔らかい素材でできているものに、ゆっくり空気を入れていくと、中の空気は膨張しますが圧力は一定のままです。つまり、体積(容積)だけ変化し、圧力は変わらないという場合です。
2-2. 仕事=圧力×体積
熱力学の第一法則には圧力を示す記号はありませんが、圧力は上記のように仕事量と関係があります。つまり仕事W、圧力P、体積Vとすると
W=PV
が成り立ちます。定圧変化では圧力を一定として仕事と体積の変化量で考えるので
ΔW=PΔV (2)
となります。
体積の代わりに比容(単位質量当たりの体積)を用いることもできます。
そこで単位質量 1kg を持つ空気塊を考えて、体積Vの代わりに比容 α をとり、先ほどの式に当てはめると
ΔW=PΔα (3)
となります。
2-3. 定圧変化を熱力学の第一法則に当てはめると
(2)の式を熱力学の第一法則の式 ΔQ=ΔU+ΔWに当てはめると
ΔQ=ΔU+PΔV (4)
同様に(3)の式を熱力学の第一法則の式に当てはめると
ΔQ=ΔU+PΔα (5)
となります。
熱力学の第一法則の式の意味を復習すると
「内部エネルギーの増加量と膨張により仕事に使われるエネルギー量との和は、空気塊に加えられる熱量に等しくなります。」(「気象予報士かんたん合格テキスト 学科一般知識編」)
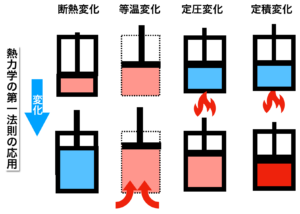
定圧変化では、熱量が一部は内部エネルギー(温度)の増加に使われ、一部は膨張のためのエネルギーとして使われるということになります。
ピストンのイメージ図(左から3番目)から分かるように、熱を加えることで温度が上昇し体積も増えるということです。
2-4. 定圧変化とシャルルの法則
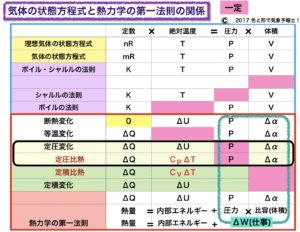
表を見てください。この表は「断熱変化と等温変化」でも載せました。
この表は熱力学の第一法則と気体の状態方程式及びボイル・シャルルの法則との関連を、要素別に示したものです。
真ん中の赤い横線より上は
定数×絶対温度=圧力×体積
が当てはまります。
赤い横線より下は
熱量=内部エネルギー+仕事(圧力×比容または体積)
が当てはまります。
黒い枠で囲った部分が定圧変化と定圧比熱の欄で、その4つ上がシャルルの法則の欄です。
どちらも圧力が一定なのでピンク色にしてあります。
シャルルの法則は、気体の圧力が一定のとき、気体の体積は絶対温度に比例することを表しています。体積をV、絶対温度をTとすると、以下が成り立ちます。
V = KT (Kは比例定数で一定)
2-5. 比熱とは
比熱とは、1g の物質の温度を1K 上昇させるのに必要な熱量のことです。
単位は JK-1g-1 で、記号はCです。
比熱の数値は物質によって特有の数値を示します。すると次の式が成り立ちます。
Q=CmΔT (6)
この式の意味は、ある物質の比熱をCとしたとき、m(g)の物質の温度をΔT(K)上昇させるのに必要な熱量はQであるということです。
比熱は熱力学の第一法則と気体の状態方程式を関連付ける役割があります。
熱力学で扱われるのは内部エネルギーです。一方、気体の状態方程式で用いられるのは絶対温度です。
熱を加えると内部エネルギーが増して温度が上昇するという理屈は分かるとして、具体的にどれだけの熱量を加えると温度が何度上昇するのかというのは分かりません。
そこで使うのが比熱です。その物質の比熱が分かっていれば、加えられる熱量と温度の上昇幅を結びつけることができます。
表を見ると比熱の欄がどうしてこうなるのか分からないかもしれません。それについてはあらためて別の記事で考えたいと思います。
2-6. 定圧比熱
では、定圧変化の場合、乾燥空気の比熱の値は幾つになるでしょうか?
定圧変化では与えられた熱量の一部は体積の増加(膨張)に使われるので、温度の上昇という点では効率が悪いことが予想されます。
「このように、乾燥空気の圧力を一定に保った状態で熱量を与えたとき、与えた熱量が空気の温度上昇と膨張の両者に使われる場合の比熱を定圧比熱といいます。」(「気象予報士かんたん合格テキスト 学科一般知識編」)
乾燥空気の定圧比熱の数値は以下となります。(Cp のp は圧力のPです)
Cp=1004JK-1kg-1 (7)
乾燥空気1kg を1K 上昇させるのに1004J のエネルギーが必要という意味です。
J(ジュール)はエネルギーの単位です。参照⇒「気象学における物理量と単位(2)」
3.定積変化
3-1. 定積変化とは
定積変化とは体積を一定とした状態変化のことです。
ガラスの箱のような硬い容器に熱を加えても、風船のように容器が膨張することはありません。想像できることですが、熱は全て温度の上昇に使われます。
定圧変化のところに載せたピストンの絵の1番右側が定積変化をイメージしたものです。
3-2. 定積変化を熱力学の第一法則に当てはめると
定圧変化のときと同様に、ΔW=PΔV(2)の式を
熱力学の第一法則の式 ΔQ=ΔU+ΔW(1)に当てはめると
ΔQ=ΔU+PΔV (4)になります。
このとき、体積は変わらない、つまり変化率がないということなので
ΔV=0 ⇒ PΔV=0
⇒ ΔW=0 よって
ΔQ=ΔU (8)
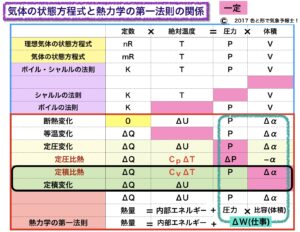
となります。表では比容α で表していますが、同様になります。
これは熱量と内部エネルギーの増加が等しいということを意味しています。
3-3. 定積比熱
「乾燥空気の体積を一定に保った状態で熱量を与えたときに、与えた熱量の全てが空気の温度上昇に使われる場合の比熱を定積比熱(定容比熱)といいます。」(「気象予報士かんたん合格テキスト 学科一般知識編」)
熱量は全て内部エネルギーの増加として使われるので、温度上昇の効率は良くなります。
乾燥空気の定積比熱の数値は以下となります。(Cv のv は体積のVです)
Cv=717JK-1kg-1 (7)
乾燥空気1kg を1K 上昇させるのに717J のエネルギーが必要という意味です。
4.定圧比熱・定積比熱と気体定数との関係
定圧比熱Cp から定積比熱Cv を引いた値は、乾燥空気の気体定数R と同じという関係があります。式にすると
Cp−Cv=R
となり、実際に計算すると、こうなります。
Cp1004JK-1kg-1 −Cv717JK-1kg-1 =R287JK-1kg-1
次回は静力学平衡に移る予定です。
