この記事では熱力学の第一法則について取り上げ、さらに熱力学の第一法則と気体の状態方程式の両方に共通する要素について調べていきます。気体の状態方程式について詳しくは「気体の状態方程式と気体定数」を読んでください。
1.熱力学の第一法則(エネルギー保存の法則)とは
1-1. 熱気球の場合
まず、イメージを掴むため、この法則を熱気球の例えを用いて考えてみます。
熱気球に火を付けると萎んでいた熱気球が膨張し、同時に中の空気の温度も上昇します。
ここで、火を熱量、膨張を仕事の結果、温度を内部エネルギーの大きさとすると、熱力学の第一法則を次のように説明できます。
1-2. 熱力学の第一法則の意味
「内部エネルギーの増加量と膨張により仕事に使われるエネルギー量との和は、空気塊に加えられる熱量に等しくなります。」(「気象予報士かんたん合格テキスト 学科一般知識編」)
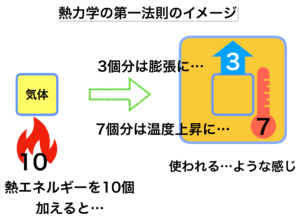
この説明を分かり易くするために、もう一つのイメージ図を紹介します。これも以前の記事で載せたものとほぼ同じものです。
つまり、内部エネルギーの増加量7と膨張に使われるエネルギー量3との和は、空気塊に加えられる熱量10に等しくなるということです。
1-3. 熱力学の第一法則の式
ΔQ=ΔU+ΔW
Δ(デルタ):変化量
Q:熱量
U:内部エネルギー
W:仕事に使われるエネルギー
2.気体の内部エネルギーとは
内部エネルギーとは分子や原子の熱運動(スピード)による運動エネルギーです。
ですから、内部エネルギーが増加すると温度が上昇します。
もう少し詳しい説明は以下の記事を参照してください。
3.仕事とは
3-1. 定義
ある物体に力F が働いて、物体が力の方向に距離S だけ動いたとき、力F はこの物体に FS=仕事W をしたことになります。つまり
仕事=力×距離 となり、式は
W = FS です。
3-2. 気体の膨張
上の式を気体に当てはめてみます。
ある球体の空気塊が周りの空気を押して(=力F)、周りの空気をもともと位置していた場所から遠ざけた(=距離S)とします。
この場合、球体の空気塊の押す力Fが周囲の空気にFS=仕事Wをしたとみなすことができます。
この仕事の結果、空気塊は 膨張した(=体積が大きくなった)ことが分かります。
※ ここではWを外部にした仕事としていますが、外部からされた仕事をWとする定義もあり、その場合 ⊿U=⊿Q+⊿Wという式で表されることが多いようです。
これ以降、Wを仕事に使われるエネルギーとすると、このエネルギーが大きいほど気体は膨張し、体積(容積)が大きくなります。
4.仕事は圧力と体積(または比容)の積
4-1. 体積の場合
仕事は圧力×体積(容積)として表すこともできます。式にすると
W=PV
となります。これを圧力を一定として仕事と体積の変化量で考えると
ΔW=PΔV
となります。
4-2. 比容の場合
ここで、体積の代わりに比容を用いることにします。
比容とは単位質量当たりの体積のことです。
そこで単位質量 1kg を持つ空気塊を考えて、体積Vの代わりに比容 α (アルファ)をとり、先ほどの式に当てはめると
ΔW=PΔα
となります。これを、熱力学の第一法則 ΔQ=ΔU+ΔW に代入すると
ΔQ=ΔU+PΔα
になります。
さて、どうして仕事を圧力と体積(または比容)の積で表せるのかは次の記事を参考にしながら、ちょっと頭をひねってください。
「気象学における物理量と単位(1)」・・体積について
「気象学における物理量と単位(2)」・・圧力について
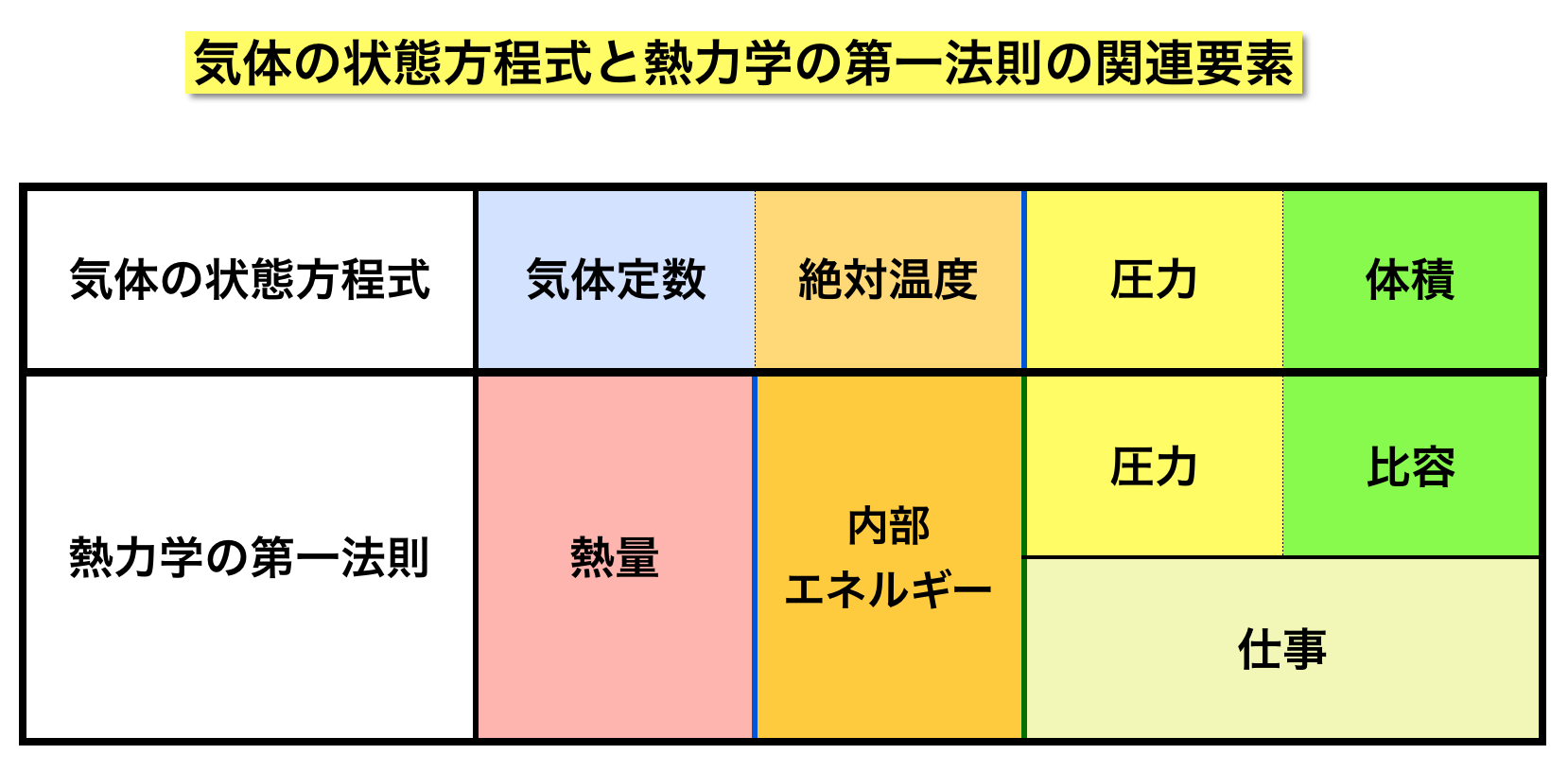
5.気体の状態方程式と熱力学の第一法則の関連要素
気体の状態方程式と熱力学の第一法則を比べてみると、それらを構成する要素に関連があるのが分かります。
表をご覧ください。気体の質量を1kg とした場合に、それぞれの要素を関連付けて示しています。
5-1. 気体の状態方程式の要素

気体の状態方程式には、質量、絶対温度、圧力、体積という物理量が含まれ、ここに気体定数が加わります。これらが要素となります。(質量は1kg なので表では省略されています。)復習すると式は
PV=mRT です。
5-2. 熱力学の第一法則の要素
一方、熱力学の第一法則には、熱量、内部エネルギー、仕事という要素が含まれています。復習すると式は
ΔQ=ΔU+ΔW です。
このうち、内部エネルギーの大小と絶対温度の高低は関連しています。
また、既に学んだように仕事は圧力と体積(または比容)の積で表すことができます。
このように気体の状態方程式と熱力学の第一法則は、気体定数と熱量は別として、他の要素は互いに関連したものであることが分かります。
これから熱力学の第一法則の応用について学んでいきますが、それぞれも気体の状態方程式と関係があることが分かっていきます。