地衡風　気圧傾度力＝コリオリ力（地衡風１）

今回取り上げる地衡風は、「４つの力と５つの風」についての一連の記事の１番目の風になります。

前半では地衡風を感覚的に捉え、後半では地衡風の求め方を取り上げています。

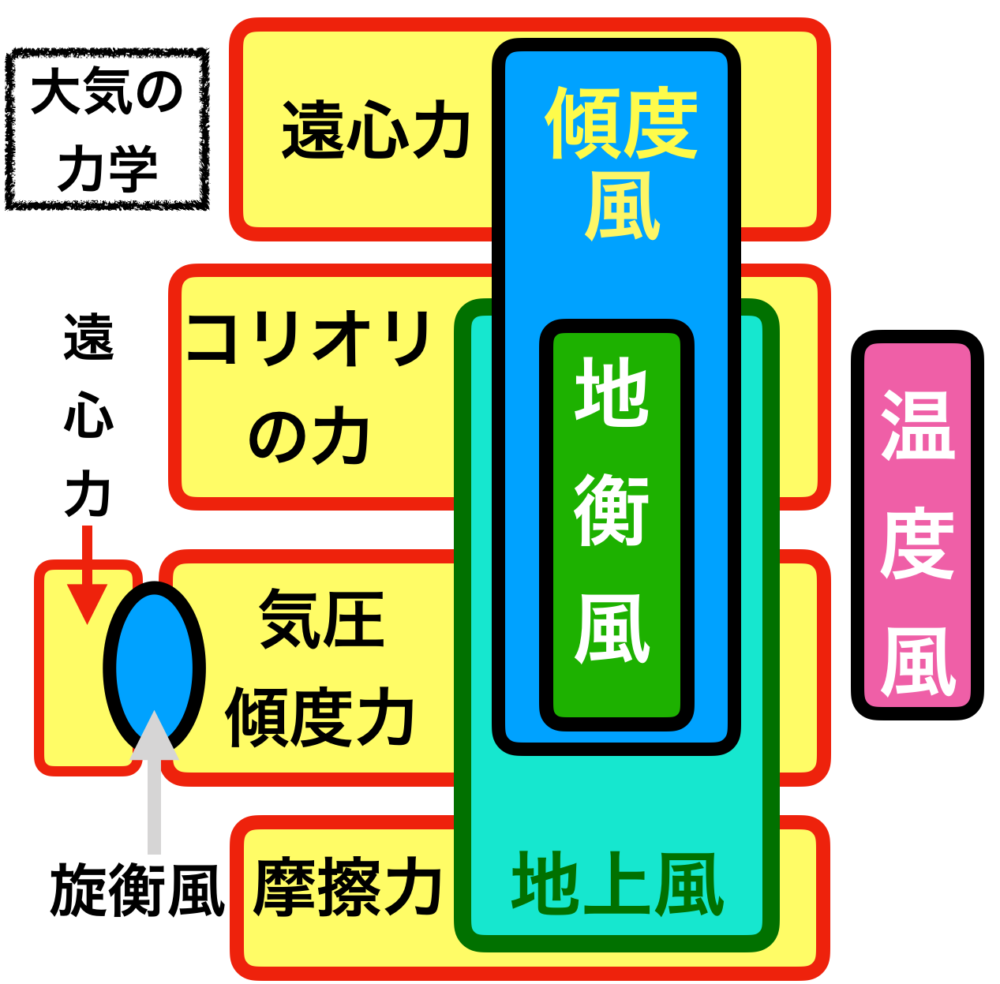
「４つの力と５つの風」については「大気の力学と運動」の記事で紹介しています。

１．地衡風を感覚的に捉える

1-1. 地衡風の立ち位置

ここからしばらくは地衡風がどのようにできるか、専門用語や数式を使わずに考えていきます。

まず、さきほど紹介した「大気の力学と運動」の記事に載せた図を見てください。

 

 

 

 

 

 

 

 

地衡風の下にはコリオリの力と気圧傾度力がありますね。

これが意味しているのは、地衡風はコリオリの力と気圧傾度力、二つの力のバランスが取れた状態で生じるということです。

1-2. 地衡風成立の概観

下記の図はどのような経過をたどって地衡風が生じるかを示しています。

 

 

 

 

 

 

 

 

大雑把に言うと高気圧から気圧傾度力によって吹き出した風がコリオリ力によって右へ右へと曲がって行き、最後には等圧線と平行に吹くようになる、という感じですね。

これが地衡風？　だいたいそうですが、もう少し順を追って解説します。

まず、前段階として風のベクトルについて確認します。

1-3. 風ベクトル 

●　風ベクトルとは　風向⇒矢印の向き、風速⇒矢印の長さ　で表現したものです。

【 コリオリ力のベクトル 】

●　コリオリ力は風のベクトルに対し直角右向きに働く（南半球では左向き）。

●　コリオリ力の大きさは風速の大きさに比例する。

 

 

 

 

 

 

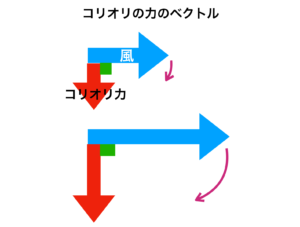
【 気圧傾度力のベクトル 】

●　風は気圧傾度力の働く方向に向かって吹く（コリオリ力を考慮しない場合）

●　風の強さは気圧傾度力の大きさに比例する。

 

 

 

 

 

 

1-4. 地衡風が生じる過程

では、ただの風が地衡風に変化する過程を考えましょう。

(1) 風の吹き始め

 

 

 

 

 

 

高気圧と低気圧との間に気圧傾度があるため、高気圧から低気圧に向けて気圧傾度力が生じます。この例では分かり易いように等圧線（縦縞）を平行であるとしています。

風は気圧傾度力により、等圧線と直角の方向へ吹き始めます。

当初は風がとても弱いのでコリオリ力は生じません。

 

(2) コリオリ力が働き始める

 

 

 

 

 

 

気圧傾度力は働き続けるので次第に風が強くなっていきます。

するとコリオリ力も風に対して働き始めます。

コリオリ力は風に対して直角に働き、風の大きさに比例して大きくなります。

コリオリ力により風の向きがやや右に変わっていきます。

 

(3) 風の向きがさらに右側に変わっていきます。

 

 

 

 

 

 

気圧傾度力により風はさらに強く吹き、コリオリ力も強くなっていきます。

 

(4) 風の向きは等圧線に対して平衡に近づく。

 

 

 

 

 

 

 

これまでと同様の仕組みで風の向きは吹き始めの時と比べると、かなり右に片寄っています。

 

(5) 地衡風が生じる。

 

 

 

 

 

 

 

 

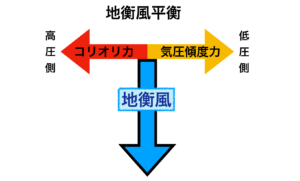
最後に風の向きは等圧線と完全に平行になり、この状態の風を地衡風と呼びます。

「最後に」と言うのは、風の向きはこれ以上 曲がることはなく、風の強さもこれ以上増すことはない、という意味です。

なぜなら地衡風が生じる段階では、気圧傾度力とコリオリ力が反対方向に、同じ大きさで働くからです。この気圧傾度力とコリオリ力がつり合った状態を「地衡風平衡」といいます。

 

 

 

 

 

地衡風は上空の風で、地上ではこのような吹き方はしませんよね。

以前の記事で西高東低冬型の気圧配置の時に、地衡風、傾度風、地上風がどのような向きで吹くかについて記事にしました。

⇒　風向きは力のバランスで決まる（西高東低の場合）

もう一度そのイメージ図を見てください。

 

 

 

 

 

 

 

 

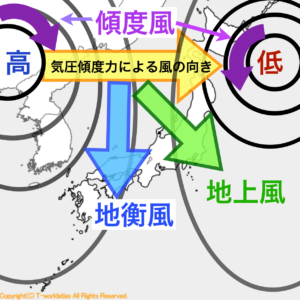
上空では地衡風は等圧線に平行に吹き、この気圧配置ではほぼ北風になっているのがわかります。

地衡風が吹くのは、おおよそ高度1000ｍ以上の上空で、それより低いと地面の摩擦の影響を受けて地上風となります。

地衡風を踏まえて傾度風、地上風もこの先 取り上げていきます。

２．２つの座標系

2-1. 地衡風の求め方は２つある

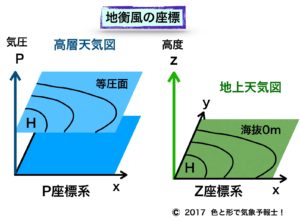
地衡風の強さの計算式には２通りあります。２つのうち、どちらの計算式を用いるかは下記の表の上段に相当するか下段に相当するかで変わってきます。

これから、この表と下のイメージ図をもとにして考えていきます。

座標系	天気図	気圧傾度力
P	高層	高度差
Z	地上	気圧差

2-2. 座標系

 

天気予報で出て来る天気図は普通、地上の気圧配置を示しています。

天気図には東西方向、南北方向が示されています。

でも実際には大気はずっと上空までつながっているので鉛直方向も考慮に入れる必要があります。

鉛直方向の表現方法によって２つの座標系に区別します。

2-3. Z座標系

鉛直方向というと普通は高度（海抜）何メートルで表します。

この鉛直方向の座標のことを高度z[m] といい、高度z を用いた座標をZ座標系と呼びます。

Z座標系の天気図が地上天気図です。

地上天気図の基準高度は海抜0m ですから、観測された気圧を海抜0m に換算して等圧線を記入します。

つまり、高度を一定にしておいて気圧の違いを線で表すということになります。

2-4. P座標系

気圧P[hPa] を高度として鉛直方向を表す方法があり、これをP座標系と呼びます。

P座標系の代表的な天気図は高層天気図です。

地上天気図に等圧線が描かれているのに対して、高層天気図では等高度線が描かれています。

つまり気圧が一定である等圧面上に高度の違いを描くということになります。

高層天気図については「等圧面って何？（高層天気図２）」をご覧ください。

３．座標系別の気圧傾度力の式

気圧傾度力の計算式は既に別の記事で取り上げていました。

この式はZ座標系を用いて気圧の差によって計算する方法です。

それに対し、P座標系を用いて高度の差によって計算する式もあります。

まとめると以下になります。

g は重力加速度ですが、なぜここで重力加速度が出て来るのかは、別のところで説明したいと思います。

４．地衡風の式

地衡風は気圧傾度力とコリオリ力がつり合って吹く風です。つまり

コリオリ力＝気圧傾度力

となります。コリオリ力の式はこちらをご覧ください。

「コリオリ力の求め方（コリオリ力４）」

 

◆　記号の意味と単位

f：コリオリパラメータ　　f=2ΩsinΦ

V：速度[m/s]

ρ：空気密度[kgm^–3]

ΔP:気圧差[Pa]

Δn：２つの等圧線（等高度線）の気圧傾度方向の距離[m]

g：重力加速度[ms^-2]

Δz：高度差[m]

 

コリオリ力＝気圧傾度力　に数式を当てはめます。

話は続くのですが、時間の関係で今日はここまでにします。近いうちに追加しますね。