1.量的予報とは
量的予報とは数値で表される予報のことで、気温、降水量の予報などが含まれます。
気象庁の量的予報についての説明を紹介します。
『気象要素を定量的に表現する予報。最高・最低気温予報、時系列予報および分布予報などがある。』
量的予報の精度評価の方法には2種類あります。
平均誤差(ME:バイアス)と2乗平均平方根誤差(RMSE)です。
それぞれの計算方法は途中まで同じです。
さっそく8月1日から5日までの5日間の最高気温の予報を例に取って考えてみます。
まずは平均誤差から。
2.平均誤差(ME:バイアス)
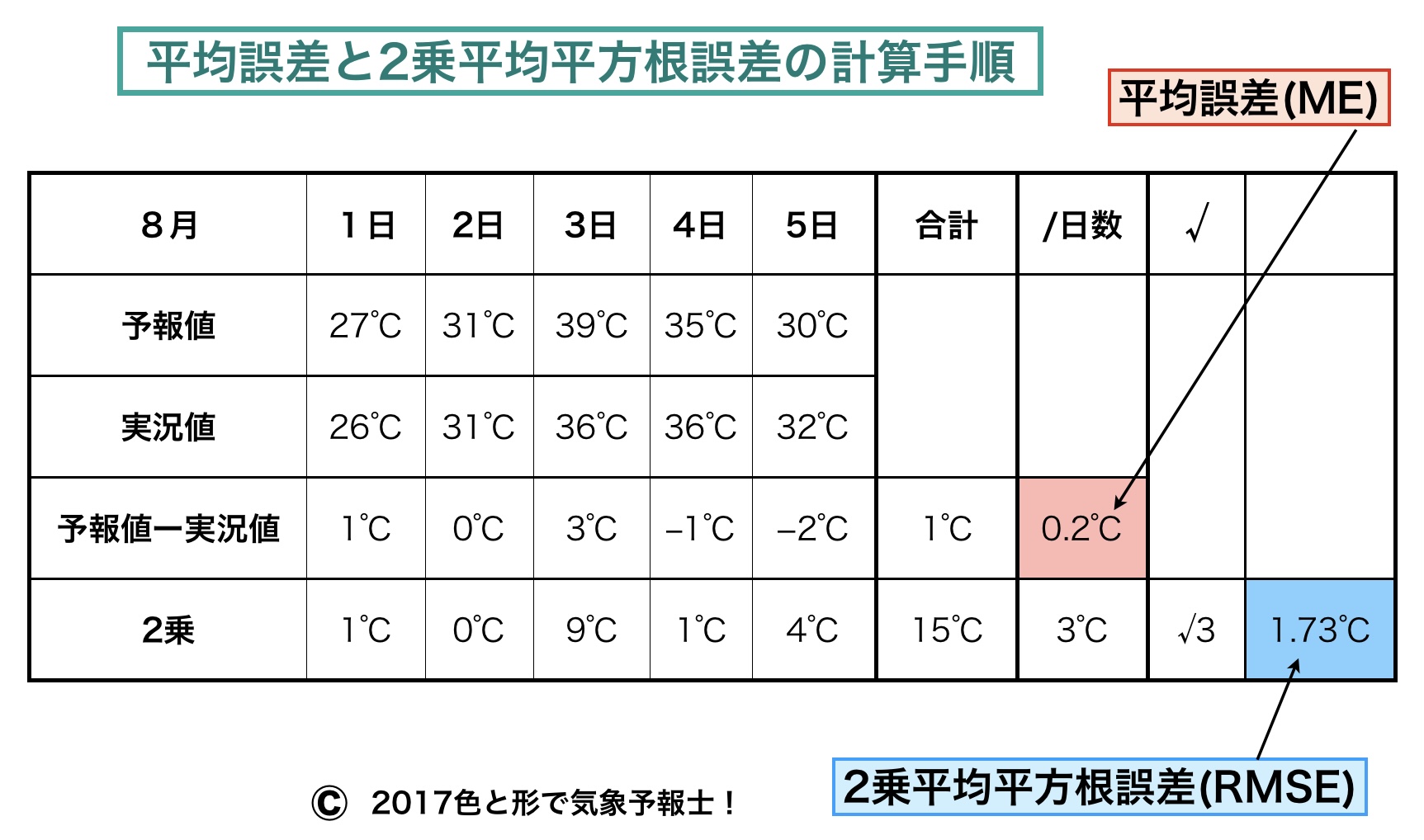
下の表をご覧ください。上段から説明します。
▶ 日付
▶ 予報値・・予報された最高気温の値
▶ 実況値・・実際に観測された最高気温の値
▶ 予報値-実況値・・誤差の値
▶ 合計・・5日間の<予報値-実況値>の値の合計
▶ /日数・・合計を日数(予報の回数)5で割った値
この値が1日(1回)あたりの平均された予報誤差になります。
これが平均誤差です。
平均誤差の別名のバイアスは偏りという意味があります。
それで、平均誤差では平均された誤差がプラス(+)に偏っているかマイナス(-)に偏っているか、その傾向を知ることができます。
3.2乗平均平方根誤差(RMSE)
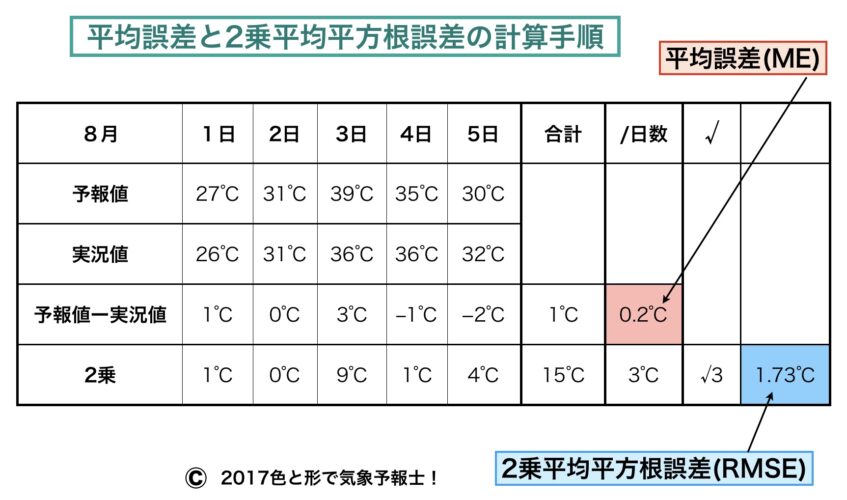
計算方法は途中まで平均誤差と同じです。最下段から説明します。
▶ 2乗・・それぞれの日における<予報値-実況値>の値を2乗
▶ 合計・・2乗した値の5日間の合計
▶ /日数・・合計を日数(予報の回数)5で割った値
▶ 上記の値に√(ルート)をかける
▶ 近似値を求めれば、この値が1日(1回)あたりの平均された予報誤差になります。
これが2乗平均平方根誤差です。
4.式
4-1. 平均誤差
$\normalsize{ME=}\large{\frac{Σ\{F(i)-A(i)\}}{N}}$
F(i):予報値 A(i):実況値 N:予報回数
Σ (シグマ)とは与えられた条件を満たす数の総和を表す記号です。本当は Σ の記号の上にn が、下に i=1 があるのですが表記が難しいので省略してあります。
値が小さいほど精度が良いことになります。
ただ、平均誤差の場合、例えば期間内に誤差が+3℃の日と-3℃の日があった場合、相殺されて誤差は0℃なってしまい、予報が外れた割には誤差の値が小さくなる傾向があります。
4-2. 2乗平均平方根誤差(RMSE)
$\normalsize{RMSE=} \sqrt{\large{\frac{Σ(F(i)-A(i))^2}{N}}}$
2乗平均平方根誤差ではマイナスの値も2乗されてプラスの値になります。
つまり、プラスの誤差とマイナスの誤差で打ち消すことがないので、より正確に誤差の大きさを判断できます。
値が小さいほど精度が良く、完全予報では0となります。
5.まとめの図
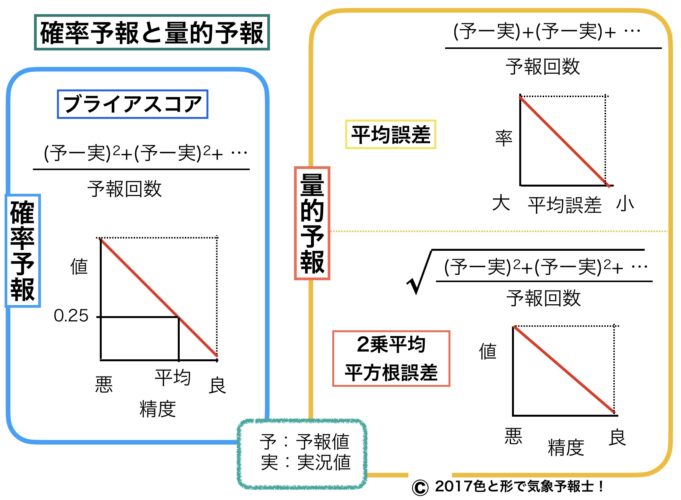
確率予報と量的予報を簡単にまとめたのが下の図です。
式も簡略化しています。この方が分かりやすいでしょうね。
6.予報の精度評価の覚え方
精度評価の種類には紛らわしいカタカナや似たような名前のものもあります。それで、おばあ様に登場していただき記憶しようということでイラストにしてみました。

▼ 確率予報(ブライアスコア)
降水確率0%だったので、ぶらぶら(ブライアスコア)散歩に出かけた。
▼ バイアススコア
婆や(バイア)が 柿見て(からぶり、きんとう、みのがし) スコ!(スコア)っと道路の穴に足がはまった。
▼ スレットスコア
(冬の東京で)雪見てスルっと(スレット)コケた(スコア)
▼ 量的予報
平気よ(平均誤差) ルーさん(ルート⇒2乗平均平方根誤差) 寒いわね(気温)
予報精度評価については以上になります。