風の発散と収束は計算式で表すことができます。
いきなり式を見ると〈なにこれ?〉状態になるので、まずは簡単なイメージ図を使って説明します。
目次
1.簡単な計算方法
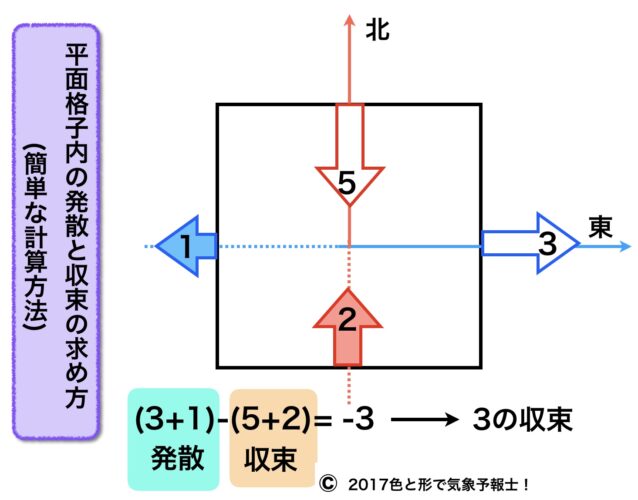
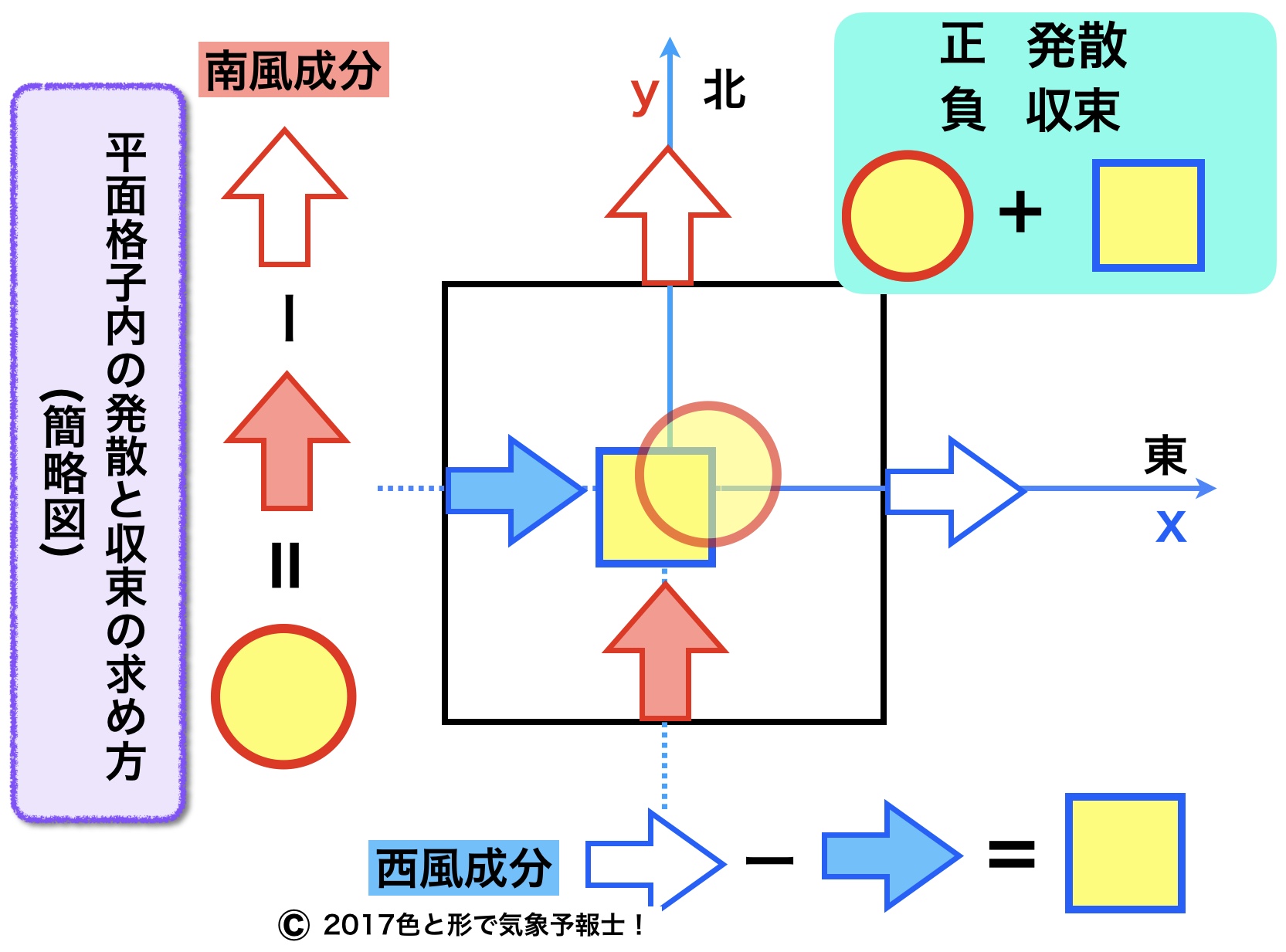
「簡単な計算方法」のイメージ図をご覧ください。正方形を平面上の一つの領域と考えます。平面格子とも言います。
この領域の上側が北、右側を東とします。
矢印はこの領域から出たり入ったりする風を表しています。数字は風速です。
では、この領域の空気は発散して量が減っているでしょうか?収束して量が増えているでしょうか?
風速を移動する空気の量に置き換えると、図の場合、正方形の領域から出て行く、つまり発散する空気の量は3+1です。一方、正方形に入って来る、つまり収束する空気の量は 5+2 です。
正方形の領域全体として考えて計算すると収束はマイナスの発散なので、
(3+1)ー(5+2)=ー3となり、これは
ー3の発散、あるいは3の収束となります。
2.数式の前提となる考え方
上記の計算で発散・収束量を求めることもできますが、数式を導き出すにはもう少し きっちりした考え方が必要になります。
2-1. 平面格子の見方
下の簡略図から説明します。
◎ 座標軸
格子の中心を通って左右に伸びる線をx軸とし、中心から右方向(東)をプラス、左方向(西)をマイナスとします。
同様に中心を通って上下に伸びる線をY軸とし、中心から上方向(北)をプラス、下方向(南)をマイナスとします。
◎ 風の成分
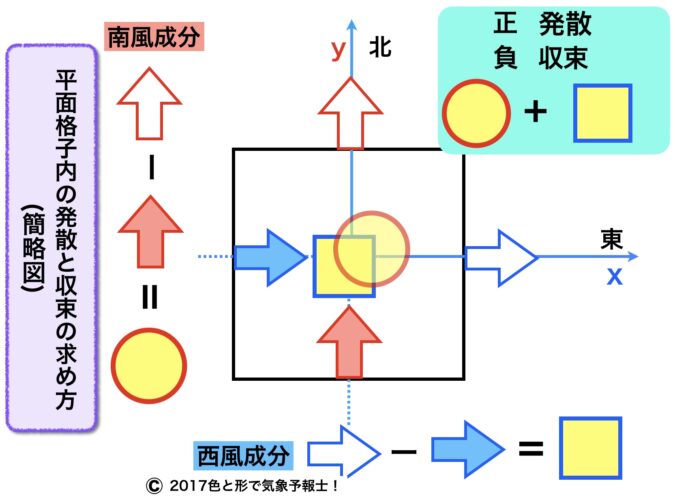
x軸に沿って東を向く矢印は格子の東側面・西側面から出たり入ったりする風の西風成分を示しています。
Y軸に沿って北を向く矢印は格子の北側面・南側面から出たり入ったりする風の南風成分を示しています。
西風成分では西風(西から東に流れる風)を正としてプラス、東風を負としてマイナスの符号を付けます。
南風成分では南風(南から北に流れる風)を正としてプラス、北風を負としてマイナスの符号を付けます。
2-2. 風の成分の差を求める
空気(風)の発散・収束は風の成分の差によって求められます。
◎ 西風成分の差
格子の東側の矢印(青枠の白)の値から西側(青)の矢印の値を引いたものが西風成分の差(青枠の黄色い四角)になります。
この差の値がプラスなら出て行く風の方が強いので、格子内の空気は東西方向において発散して空気の量は少なくなっているといえます。
マイナスなら入って来る風の方が強いので、収束して空気の量は増えています。
◎ 南風成分の差
同様にして南風成分の差(赤枠の黄色い丸)を求めれば南北方向における発散・収束量を知ることができます。
2-3. 格子領域内の発散・収束量
西風成分の差で求めた発散・収束量と南風成分で求めた発散・収束量を合計すれば領域全体の空気量の増減が分かります。
合計した数字がプラスなら発散、マイナスなら収束、0なら発散も収束もないことになります。
以上が発散・収束の計算の仕方の基になる考え方です。
3.計算例
言葉だけで説明しても分かりづらいので数字を当てはめて計算してみます。
この場合、格子の側面から出ている外向き・内向きの矢印は格子に出入りする風の向きと強さを表し、数字は風速を示しています。
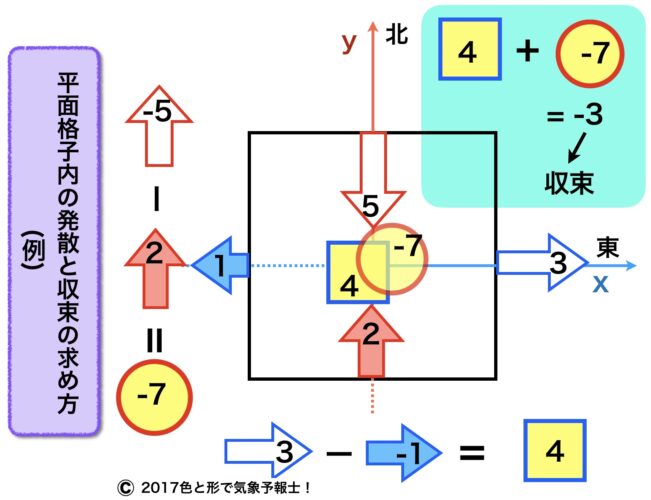
3-1. 西風成分の計算
x軸方向の風の向きと強さをもとに西風成分の差を計算すると
(+3)-(-1)=(+4)
となるので、東西方向の発散量は4です。
3-2. 南風成分の計算
同様にY軸方向で南風成分の差を計算すると
(-5)-(+2)=(-7)
となり、南北方向では発散量が-7または収束量が+7になります。
3-3. 格子全体の発散量
西風成分と南風成分の合計が全体の発散量になります。
(+4)+(-7)=(-3)
ですから、発散量が-3、収束量が+3です。
4.発散・収束の計算式の導き方
ここまでの基本的な考えをもとに、発散・収束の式がどのようにして導き出されるかを考えていきます。
4-1. 座標軸と風の出入り
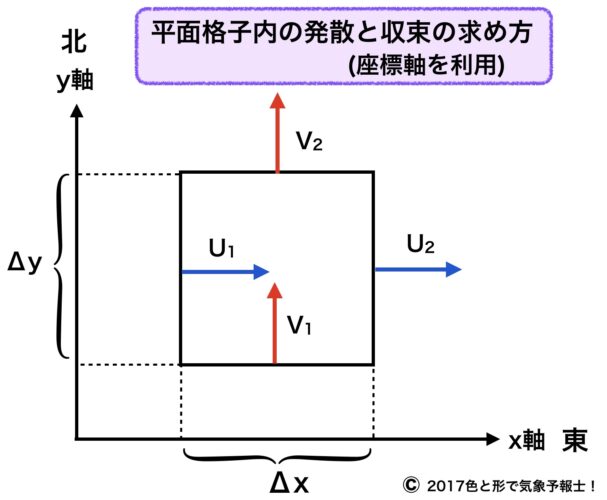
下の図をご覧ください。
これまでと違ってX軸・Y軸を平面格子(青い正方形)の外に取ります。
この正方形はΔXとΔYに囲まれた領域になります。
また、この領域に吹く風を西風成分u と南風成分v に分けます。
そして、正方形の東西の側面からu1,u2 の風、南北の側面からv1,v2 の風が吹いているとします。
4-2. 水平発散・水平収束
この領域に出入りする単位時間、単位面積当たりの大気の収支を水平発散または水平収束といいます。
この領域において空気の流入量より流出量の方が多い場合は領域内の空気は減少します。これが水平発散(発散)です。
逆に流入量の方が多い場合は領域内の空気は増加します。これが水平収束(収束)です。
では、この領域の東西方向・南北方向に吹く風による1秒当たりの空気の増減量を計る計算式を調べていきます。
4-3. 計算式の基本的な考え方
発散・収束の簡略図では格子内を通る風を1本の線で表現していました。
でも実際には風は幅のある側面全体から出たり入ったりするので、風速に側面の長さを掛け合わせて出入りする空気の量を測ります。その点を考慮して計算式を求めていきます。
4-4. 東西方向の空気の増減量
◇ 西風成分の差をΔu とすると Δu=u2-u1 です。
◇ 空気の増減量
西風成分の差に南北の側面の長さ(Δy)を掛けます。
(u2-u1)Δy=u2Δy-u1Δy
4-5. 南北方向の空気の増減量
◇ 南風成分の差をΔv とすると Δv=v2-v1 です。
◇ 空気の増減量
南風成分の差に東西の側面の長さ(Δx)を掛けます。
(v2-v1)Δx=v2Δx-v1Δx
4-6. 領域全体への空気の流入・流出量
正方形の領域への1秒間に単位面積当たりに流入・流出する空気の総量をD[1/s]とすると
発散・収束量D[1/s]=増減した空気量[m2/s] / 面積[m2]
$D[1/s]=\large{\frac{(u_2Δy-u_1Δy)+(v_2Δx-v_1Δx)}{ΔxΔy}}$
$=\large{\frac{u_2Δy-u_1Δy}{ΔxΔy}+\frac{v_2Δx-v_1Δx}{ΔxΔy}}$
$=\large{\frac{u_2-u_1}{Δx}+\frac{v_2-v_1}{Δy}}$
$=\large{\frac{Δu}{Δx}+\frac{Δv}{Δy}}$
これが水平発散・水平収束の式になります。
5.まとめ
水平発散・水平収束の式
$\color{blue}D[s^-1]=\large{\frac{Δu}{Δx}+\frac{Δv}{Δy}}$
Dは発散・収束量
D>0:発散 D<0:収束
上の式を言葉で表すとこのようになります。
$\color{blue}発散量=\Large{\frac{西風成分の差}{東西の距離}+\frac{南風成分の差}{南北の距離}}$
の式をちょっといじると渦度の式になります。渦度については別の機会に。
1つの問題に発散・収束と渦度の両方を求めるものもあるようなので、セットで覚えたいですね。ではまた。。。