雲粒や雨粒は成長し質量が増すと上昇気流で支えることができなくなり落下していきます。
重力があるので落下速度は加速していき最後には雨粒は傘を突き破って痛い目に合います(かも)。
そうならないのは降水粒子の落下速度に上限があるからです。今回はその点を調べていきます。
目次
1.終端速度
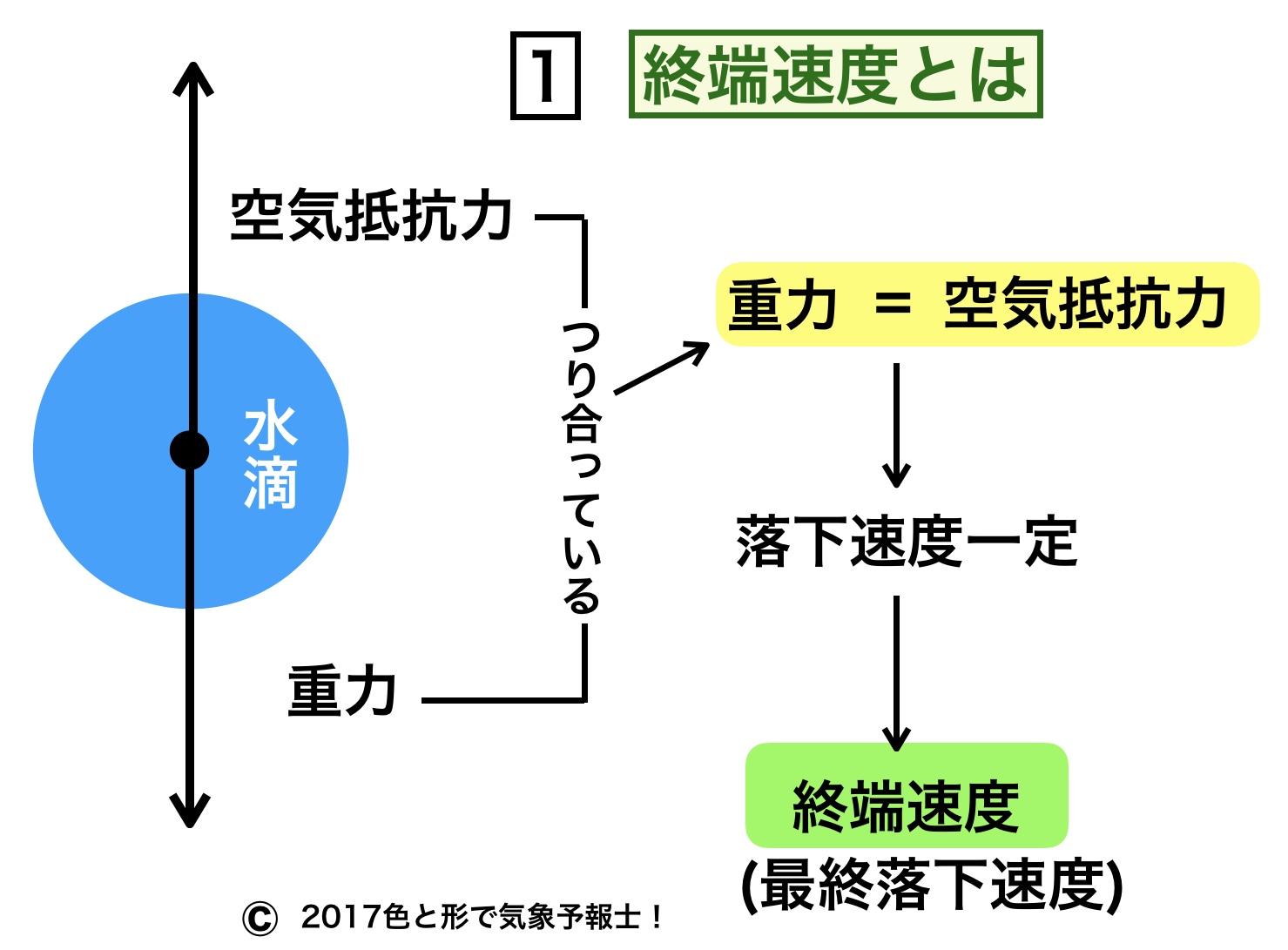
雨粒や雲粒などの落下速度を抑えるのは空気抵抗(摩擦)です。
空気抵抗は空気の粘り具合と落下する物体の断面積で決まる物理量です。
空気には粘り気があるので落下する物体には空気抵抗が働きます。
空気抵抗力(摩擦力)は重力と反対方向(上向き)に働き、落下速度が増すに連れて大きくなります。
するとある時点で重力と空気抵抗力が等しくなり落下速度は一定になります。
この時の速度を終端速度(または終末速度)あるいは最終落下速度といいます。冒頭の模式図はここまでの説明をまとめたものです。
2.半径から重力へ(概要)
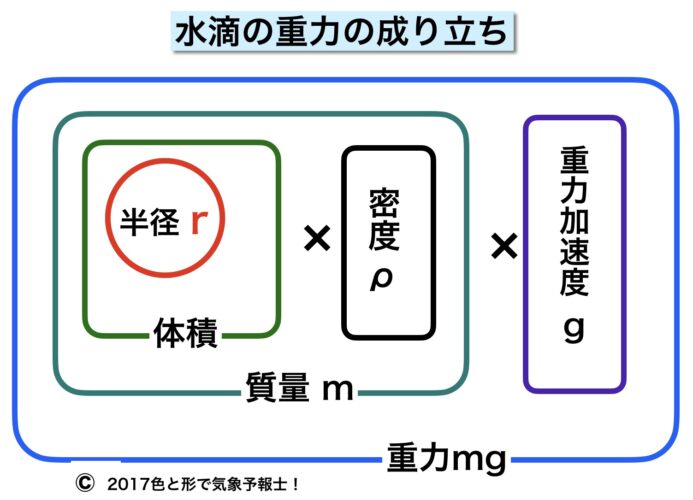
まずは降水粒子に働く重力をどのように求めるか考えていきます。
この図は球形の降水粒子の半径が重力とどのようにつながっているかをおおまかに示したものです。
まず、半径r が決まれば降水粒子の体積も決まります。
体積に水滴の密度ρ を掛けると質量m が決まります。
質量m に重力加速度g を掛けた値が重力mg になります。
3.半径から重力へ(数式)
上の流れを数式を使って降水粒子に当てはめたのが下の図です。(単位は省略、以下同様)
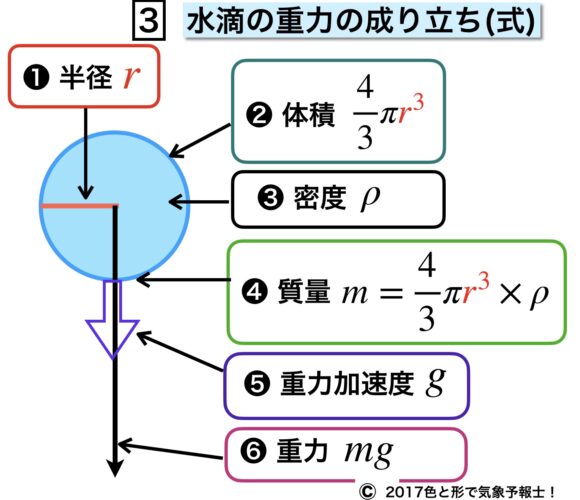
この式から重力は $\large{\mathit{mg}}=\dfrac{4}{3}\Large{\pi\color{red}r^{3} }\large{\rho\times \mathit{g}}$ とも表せることが分かります。
4.雲粒にかかる空気抵抗力(概要)
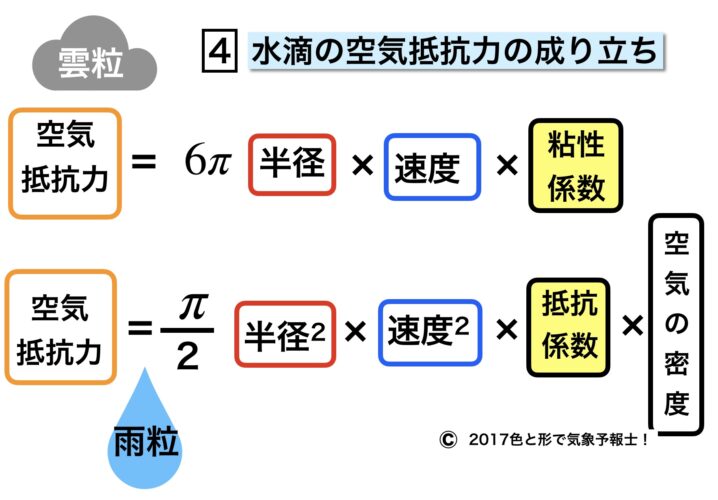
この図の上段が雲粒で下段が雨粒です。まず雲粒について説明します。
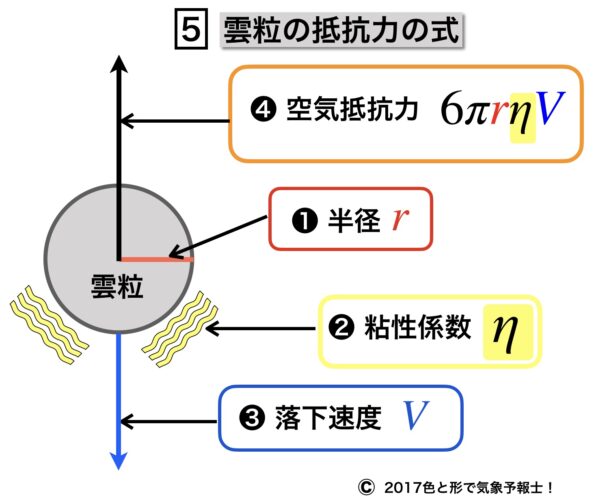
空気抵抗力に関係するのは雲粒の半径と落下速度、それに粘性係数です。
粘性係数は空気や液体などの流体の粘り気の度合いを表すものです。つまり、サラサラしているか粘っこいかを示しています。
記号は η (イータまたはエータ)です。
雲粒には粘性抵抗が働きます。
粘性抵抗は物体の速度が極めて遅いときに働く抵抗で、速度に比例します。
雲粒と雨粒で違いが出るのは雨粒が雲粒より大きく空気抵抗が大きいからです。雨粒については後述します。
5.雲粒にかかる空気抵抗力(数式)
6.雲粒の終端速度
雲粒にかかる重力と空気抵抗力がつり合ったときの速度が終端速度なので、次の式が成り立ちます。
$$\large{\mathit{mg}} = 6\Large{\pi\color{red}r}\color{black}\eta\mathit{\color{blue}V}$$
この式に $\mathit{mg}=\dfrac{4}{3}\Large{\pi\color{red}r^{3} }\large{\rho\times \mathit{g}}$ を当てはめて整理すると
$$\large{\mathit{\color{blue}V}}=\large{\frac{2\Large\color{red}{r}^{2}\color{black}\rho\mathit{g}}{9\eta}}$$
となり、ここから次の関係が導き出されます。
$$\large{\mathit{\color{blue}V}} \propto \Large{\color{red}r^2}$$
$\propto $ は比例記号で、左右が比例関係にあるという意味です。
つまり、雲粒の終端速度は雲粒の半径の2乗に比例するということです。
ですから雲粒の半径が2倍になれば終端速度は4倍になります。
7.雨粒にかかる空気抵抗力(概要)
先ほどの「4 水滴の空気抵抗力の成り立ち」の図を見てください。
下段が雨粒に対する空気抵抗力を示しています。
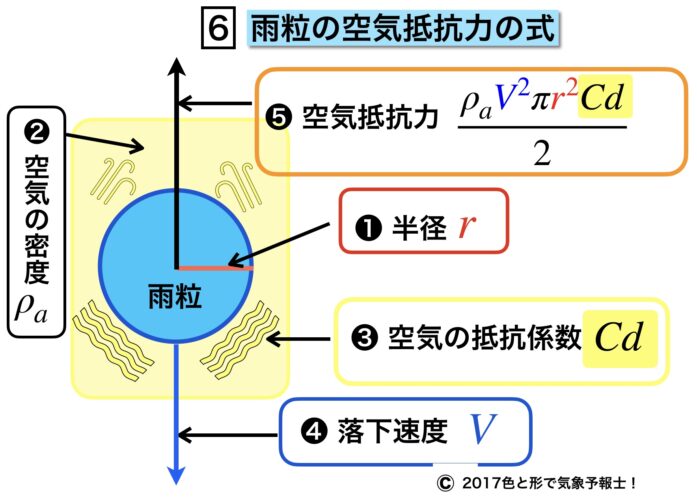
雲粒の場合と違うのは空気の密度 ρa が関係することと粘性係数の代わりに空気の抵抗係数Cd が用いられているという点です。
雨粒には慣性抵抗が働きます。
慣性抵抗は物体の速度が速いときに働く抵抗で、速度の2乗に比例します。
8.雨粒にかかる空気抵抗力(数式)
これに数式を当てはめたのが下のイメージ図です。
9.雨粒の終端速度
雨粒にかかる重力と空気抵抗力がつり合ったときの速度が終端速度なので、次の式が成り立ちます。
$$\large{\mathit{mg}} = \large{\frac{\rho_a\color{blue}\mathit{V}^{2}\color{black}\pi\color{red}r^{2}\color{black}\mathit{C_{d}}}{2}}$$
この式に $\large{\mathit{mg}}=\dfrac{4}{3}\Large{\pi\color{red}r^{3} }\large{\rho\times \mathit{g}}$ を当てはめて整理すると次の式が成り立ちます。
$$\large{\mathit{\color{blue}V}^{2}} = \frac{8}{3}\times\dfrac{\Large{\color{red}r}\large{\color{black}\mathit{gρ}}}{\mathit{C_{d} ρ_a}}$$
V について解くと次の関係が導き出されます。
$$\large{\mathit{\color{blue}V}} \propto \color{red}\sqrt{r} \color{black}\normalsize{または} \large{\mathit{\color{blue}V}} \propto \Large{\color{red}r^{\frac{1}{2}}}$$
つまり、雨粒の終端速度は雨粒の半径の平方根に比例するということです。
例えば、終端速度は雨粒の半径が2倍になれば√2倍(約1.41倍)、3倍になれば√3倍(約1.73倍)になります。
雨粒は雲粒より大きく空気抵抗が大きいため、雲粒に比べて半径の増加に対して落下速度の増加の割合が小さくなっています。
10.まとめ
▶ 終端速度・・重力と空気抵抗力がつり合って速度が一定となったときの落下速度
▶ 雲粒の場合
◎ 落下速度と空気抵抗力がつり合ったときの式
$$\large{\mathit{mg}} = 6\Large{\pi\color{red}r}\color{black}\eta\mathit{\color{blue}V}$$
◎ 雲粒の終端速度は雲粒の半径の2乗に比例 $\large{\mathit{\color{blue}V}} \propto \Large{\color{red}r^2}$
▶ 雨粒の場合
◎ 落下速度と空気抵抗力がつり合ったときの式
$$\large{\mathit{mg}} = \large{\frac{\rho_a\color{blue}\mathit{V}^{2}\color{black}\pi\color{red}r^{2}\color{black}\mathit{C_{d}}}{2}}$$
◎ 雨粒の終端速度は雨粒の半径の平方根に比例
$$\large{\mathit{\color{blue}V}} \propto \color{red}\sqrt{r} \color{black}$$