日々 目にする天気図の中で平行な等圧線というのはあまり見かけませんね。
高気圧や低気圧の周りの等圧線は湾曲しています。台風に至ってはほぼ円形です。
このような気圧配置では、上空で地衡風に遠心力を加えた風、つまり傾度風が吹いています。
では遠心力とは何か?それが今回のテーマです。
以前の記事「大気の力学と運動」(2018/05/11)で載せた、「大気の力学」という図をご覧ください。この中の4つの力のうちの1つが遠心力です。

1.身近にある遠心力
「注意‼ 急カーブ!」
遠心力とは何か?これはコリオリの力と違って日常生活で体感するものです。
例えば車の運転で。カーブの時に。
伊豆半島のように山が海に迫り出した地形では、S字状になった道が多いです。
緩やかなカーブだとあまり怖くないですが、急カーブだと車が道路からカーブの外側の崖にはみ出して海に投げ出されそうでスリルがあります(安全第一!)。遠心力を感じます。
また、同じカーブでも車のスピードを出していると、余計に外側に投げ出されそうな感覚を覚えます。なので普通はカーブに差し掛かる前に速度を落とします。
このことから遠心力の性質が分かります。
1.遠心力は中心から外側に働く。
2.カーブがきついほど強い。
3.スピードが速いほど強い。
2.曲率
カーブがどれくらい きついかは曲率で表現します。
半径r の円の曲率は・・ \(\frac{1}{r}\)
半径r が分母にあるので、こうなります。
円が大きい⇒ 曲率は小さい=カーブがゆるやか
円が小さい⇒ 曲率が大きい=カーブがきつい
3.遠心力の式
半径r の円周上を速度Vで運動している質量m の物体にかかる遠心力は、
$$遠心力=\frac{mV^{2}}{r}$$
です。気象学では単位質量の空気として考えるので、m=1 とすれば
$$遠心力=\frac{V^{2}}{r}$$
となります。言葉にするとこうなります。
$$遠心力=\frac{風速^{2}}{半径}$$
この式から、遠心力は速度の2乗に比例し、半径に反比例することが分かります。
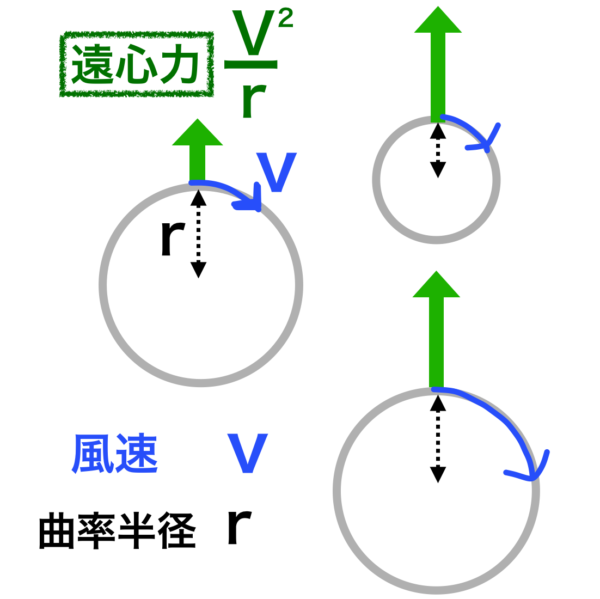
これをイメージ図を使って考えると、こうなります。
◎風速は同じ 円の半径(r)が小さくなる
⇒遠心力は大きくなる(右上の円)
◎円の半径が同じ 風速が大きくなる
⇒遠心力は大きくなる(右下の円)
次回は地衡風に遠心力がかかって生じる傾度風を考えます。