1.傾いているのは変?
エマグラムでは空気中の水蒸気量を表すために混合比を用いています。
具体的には空気が飽和するときの混合比、つまり飽和混合比を示す等飽和混合比線から読み取るようになっています。
でも、この線がなぜ傾いているのか疑問に思ったことはないでしょうか?
混合比が温度・気圧・体積・密度が変わっても保存されることは既に学びました。
でも飽和混合比となると、飽和水蒸気圧・飽和水蒸気密度は温度の関数なので、飽和混合比も温度の関数であるはずです。ですから飽和混合比は温度に関しては保存されないといえます。
そうであれば等しい飽和混合比はどの高さでも温度が一定でなければなりません。
実際は等飽和混合比線は高度が増し気圧が低くなるに連れて低温側に傾いていきます。なぜ?というのが今回のテーマです。
2.文章で説明すると
ちょっと前置きが長くなりましたが、いきなり結論に入ります。
水蒸気密度で考えてみると飽和混合比の式は以下の通りです。
飽和混合比=飽和水蒸気密度 / 乾燥空気密度
ここで高度が変わって気圧が変化すると、乾燥空気密度も変化します。
飽和混合比が一定で乾燥空気密度が変化するとなると飽和水蒸気密度も変化しなければなりません。
飽和水蒸気密度は温度の関数なので、飽和水蒸気密度が変化するなら飽和するときの温度、露点温度も変わるはずです。というのが文章で書いた結論です。
まあ、そうなんだろうけど視覚的に掴みたいなという訳で例によって模式図を使って説明します。
等飽和混合比線は作図上傾きを大きくしています。また、図の中の数字は解説しやすいように概数で書かれていて正確ではありませんので、予めご了承ください。
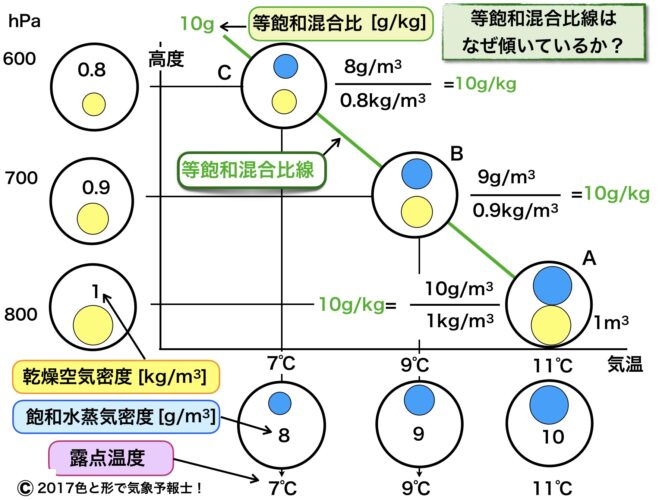
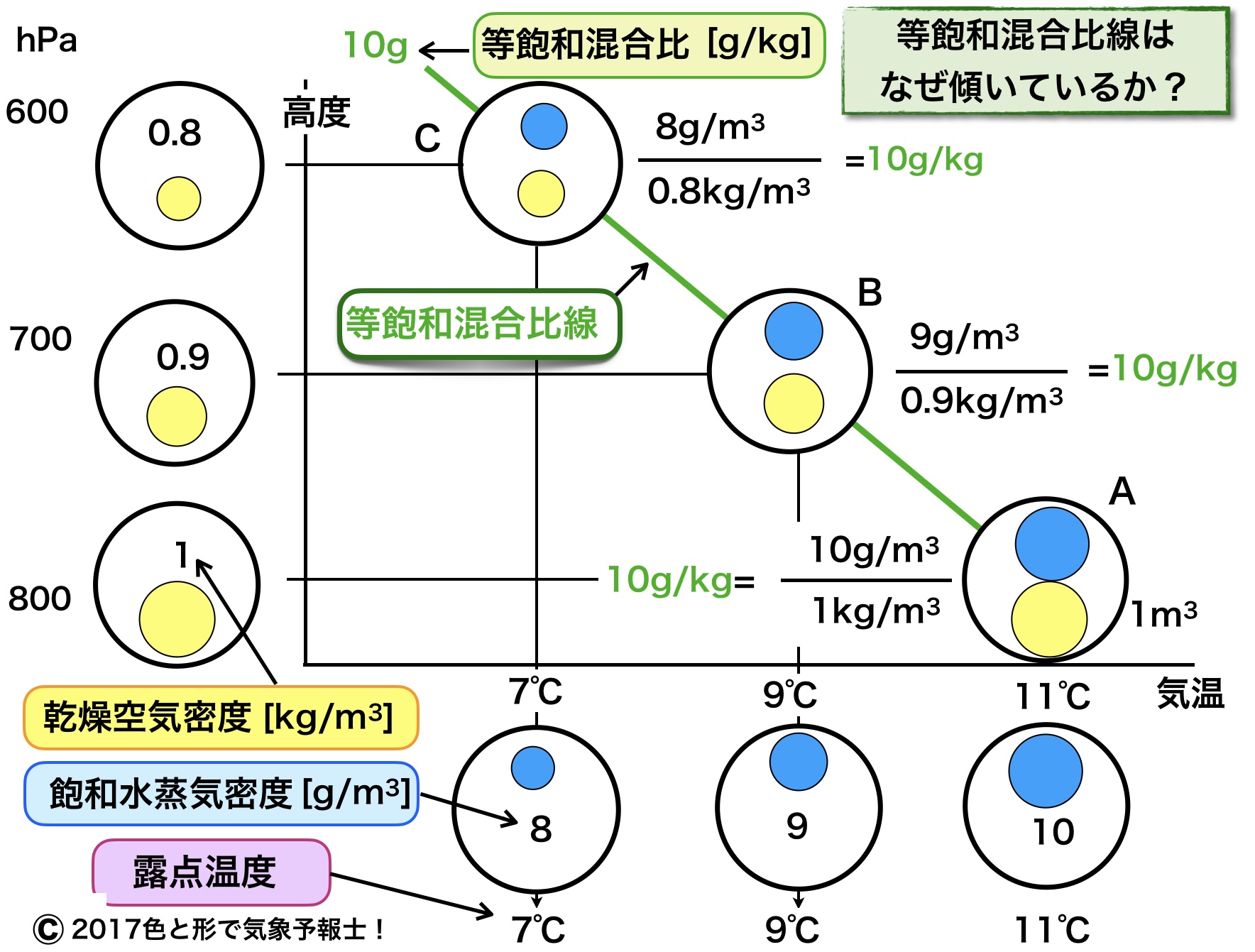
3.飽和混合比を算出する
図の右下の空気Aを見てください。Aは湿潤空気で体積を 1m3 とします。
気温の軸を見ると、Aは 11℃ で飽和に達しました。ですから露点温度は11℃ です。
温度と飽和水蒸気密度の関係から A には10g の水蒸気が含まれていて飽和水蒸気密度は 10g/m3 だと分かります。
次に高度の軸を見てみます。
空気A は 800hPa 付近にあって乾燥空気密度は 1kg/m3 です。これで A の飽和混合比は以下の計算式で求められます。
10g/m3 ÷ 1kg/m3 = 10g/kg
4.高度を変えると
次に気圧高度 700hPa 付近に注目します。この高度で空気Aと同じ飽和混合比の空気はどこにあるのでしょうか?
この高度の乾燥空気密度は 0.9kg/m3 なので飽和水蒸気密度は次の式で算出できます。
10g/kg = xg/m3 ÷ 0.9kg/m3 ⇒ x =9
飽和水蒸気密度 9g/m3 に対応する露点温度を見ると 9℃ だと分かります。高度と露点温度が交わったところにある空気B がAと同じ飽和混合比を持つことが分かります。
同様にして 600hPa 付近で飽和混合比がAと同じになるのは空気Cです。
A、B、Cを結べば 10g/kg の等飽和混合比線の出来上がりです。
A、B、Cを比べると水蒸気量が違うように見えますが、混合比は比率で水蒸気量を表す方法なので、問題ないのです。
このように考えていけば等飽和混合比線が傾いている理由をはっきり理解できます。
気温と気圧と水蒸気量の3つを一つの図にまとめるって、どなたが考え付いたのか知りませんが、よくできていますね。