ここでは地球全体として受ける太陽放射の強さに何が関係しているかについて考察します。
次いで地表面が受ける放射強度の求め方の基本を学びます。
目次
1.地球が受ける太陽放射
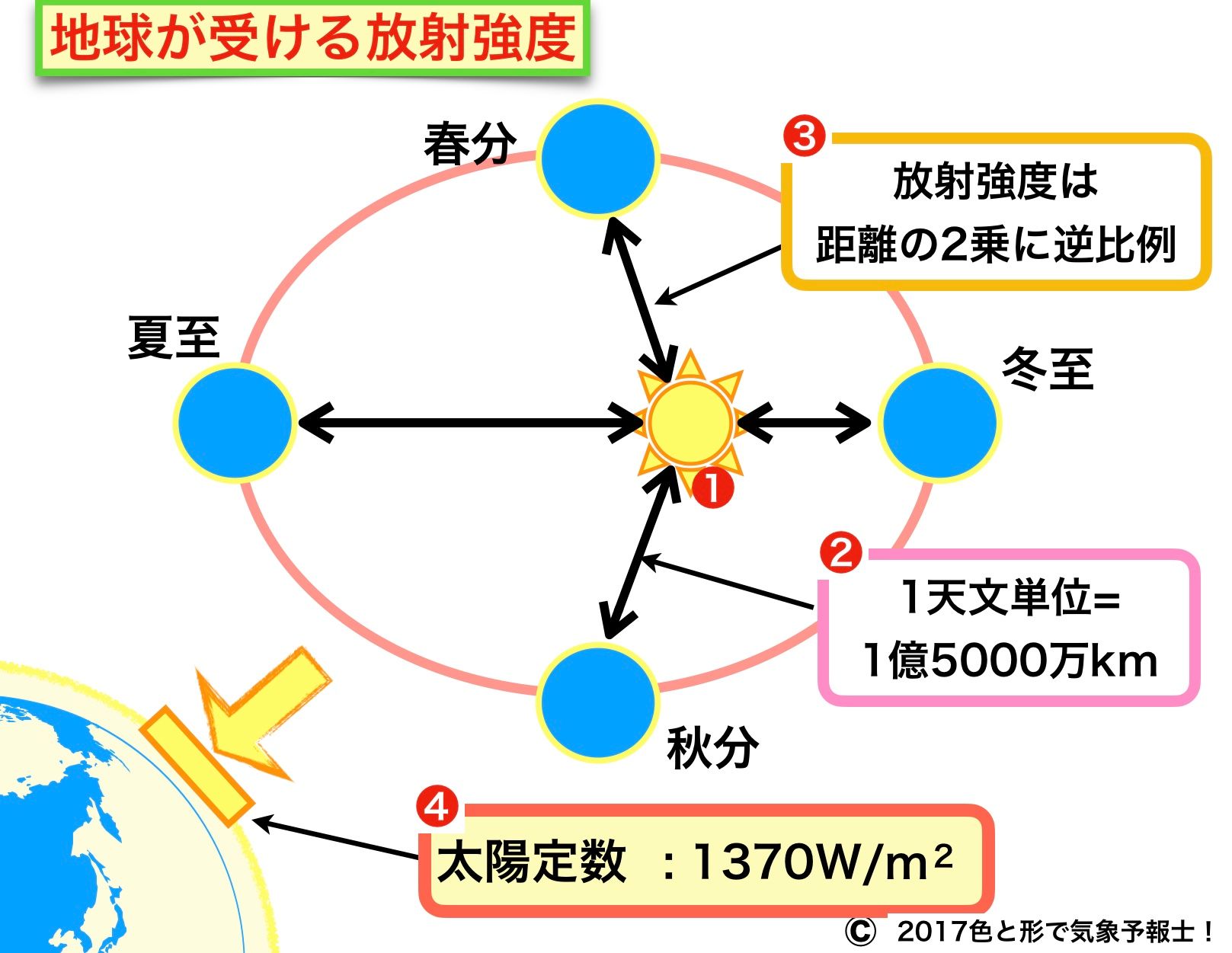
地球が受ける太陽放射の強さに関わる要素について下のイメージ図の番号順に説明します。
❶ 太陽放射
太陽表面の黒体放射温度は5780K(約6000K)です。
そして太陽から放射される電磁波のほとんどは広義の光である紫外線、可視光線、赤外線です(前回の記事を参照)。
その中でもおよそ半分を狭義の光である可視光線が占めていて、最も放射強度が強くなっています。
❷ 太陽からの距離
太陽と地球との平均距離はおよそ1億5000万km で、この距離を1天文単位といいます。
「平均」と付けたのは図にあるように地球の公転は楕円形になっていて季節によって距離が変わるからです。この点は別記事で取り上げます。
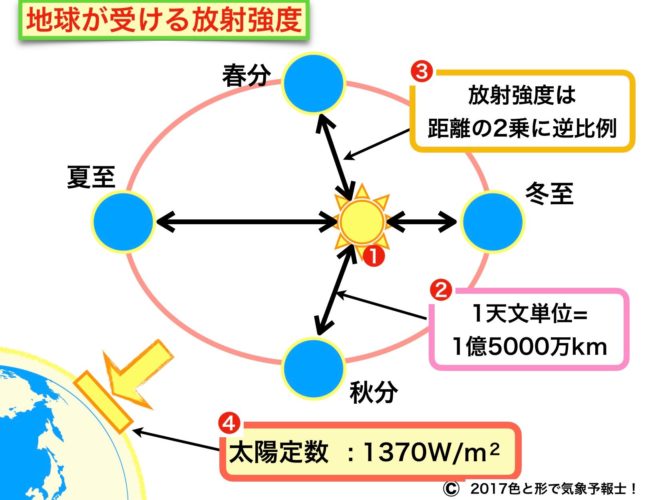
❸ 放射強度と距離の関係(距離の逆2乗則)
放射強度は距離の2乗に逆比例(反比例)するという法則があります。
距離が2倍になれば放射強度は4分の1になるということですね。
❹ 地球が受ける太陽放射強度(太陽定数)
以上が分かれば地球全体が受け止める太陽放射の強さが導きだされます。
全体で受ける数値は別の記事で紹介します。ここからは気象学に直接かかわる、地球上の単位面積あたりの放射強度(太陽定数)について考えます。
● 太陽定数とは・・地球の大気上端で太陽の方向に垂直な単位面積(1m2 )で1秒間に受ける太陽放射エネルギー量
● 太陽定数(数値)・・・
1370Wm–2 = 1.37kWm–2 = 1.37×103Wm-2
テキストによっては
1380Wm–2 = 1.38kWm–2 = 1.38×103Wm-2 としているものもあります。
W(ワット)とは1秒に1J(ジュール)の仕事をする仕事率のことです。詳しくはこちらの記事を参照してください。
⇒ 「気象学における物理量と単位(2)」
2.地表面が受ける太陽放射強度
2-1. 空気は無視して
地球上のそれぞれの場所における太陽放射強度を知るには もっと複雑な計算が必要になりますが、まず基本を押さえておきます。
さきほど出てきた太陽定数には「大気の上端における」という但し書きがついています。実際には太陽光が地表に届く間には大気による吸収などがあるため、地表に達する放射強度は弱くなります。
このあたりの仕組みについては別のところで扱いますが、ここではひとまず大気の存在を無視して考えていきます。
2-2. カギは太陽の高さ
地表面が受ける放射強度は太陽の高さによって違ってきます。
これは感覚的にわかると思います。夏は太陽が高く日差しが強いので、ひなたでは熱く感じます。冬はその逆になります。同様のことは朝・夕と真昼といった1日の中の時間帯による違いにも当てはまります。
2-3. 太陽の高さと日の当たる範囲
下のイメージ図を見てください。
◆ 太陽が真上にある場合(図の左上)
太陽の光が上空から円形に降り注ぐと仮定すると、地表面での光の当たり方は上空と同じ大きさの円形になります。
日の当たる範囲は狭いですが日差しは強く感じます。
◆ 太陽の高さが低い場合(図の左真ん中)
太陽の光は地表に当たらないうちは円形に進みますが、地表面に達すると光の当たる範囲は広く楕円形になります。
日の当たる範囲は広くなりますが、その分 日差しは弱く感じます。
実際、夏の日差しは強いですがあまり窓から部屋の中には入ってきません。対して冬は日差しは弱いものの部屋の奥の方まで入ってきます。
◆ 光の量は同じ
日差しの強弱はあっても降り注ぐ光の全体の量はどちらも変わりません。

2-4. 直角三角形を用いたイメージ図の説明
さきほどの例えと同様の考え方を直角三角形を用いて表したのがイメージ図の左下の図です。これは地表面を真横から見たものです。
光の当たる範囲は本来2次元(面積)で表しますが、この図では1次元(長さ)に置き換えて表現しています。(長さは線または細長い長方形で表現しています)
少し説明を加えます。
● 上空の赤い長方形・・太陽定数
● 高度角 α (アルファ)・・
太陽光の入射する方向と地表面との角度
● 地表面の赤い長方形と黄色の長方形・・
太陽光の当たる範囲
2-5. 単位面積(1m2)当たりの放射強度の考え方
◆ 太陽光が地表に垂直に当たる場合
光が真上から差し込む場合は地表を照らす光の面積は上空と同じです(赤い長方形)。
ですから単位面積(1m2 )で受ける放射強度(太陽放射のエネルギー量)は太陽定数と同じ数値になります。
◆ 斜めから差し込む場合
光が斜めから差し込む場合は、日の当たる範囲は広くなります(黄色の長方形)。
この場合、単位面積(1m2)当たりの放射強度を知るには、太陽定数を地表の面積(m2)で割る必要があります。
直角三角形に当てはめると短い辺を長い辺で割ることで計算できます。

2-6. 三角関数を利用する
左下の直角三角形の向きを変えたのが図の右下の直角三角形です。
短い辺(太陽定数)を a 、長い辺(地表面)を b とすると、
単位面積(1m2)当たりの放射強度は、太陽定数÷地表の面積 ですから、
$\Large{\frac{a}{b}}$ となります。
ただ、地表の面積をいちいち測るのも面倒なので、高度角 α を用いることにします。
三角関数を使えば、$\Large{\frac{a}{b}}$ はsin α に置き換えることができます。まとめると次の式になります。
地表面が受ける放射強度=太陽定数× sin α
たとえば太陽高度角が30度の場合、sin30° = 1/2 なので、放射強度は
1370W/m2 × sin30° = 685W/m2 になります。
太陽が真上にある時は太陽高度角は90度で sin90° = 1 なので、放射強度は
1370W/m2 × sin90° = 1370W/m2 になります。
* 三角関数については以下の資料を参照してください。
「気象予報士かんたん合格テキスト(技術評論社)」巻末の付録「数学の基礎」
ここまでが地表面が受ける放射強度の基本となります。
次回は、この基本を踏まえてさらに季節や緯度によって放射強度がどう変わるかに取り掛かっていきます。