今回は静力学平衡の式の応用として、海面更正(海面補正)の式と測高公式を取り上げます。
これら2つの式はどちらも層厚の考え方を当てはめていますが、アプローチの仕方が違っています。
海面更正の式は標高と温度から海面高度の気圧を求めるのに対し、測高公式は気圧と温度から高度を求めるものです。
言い換えれば、海面更正の式は上から下、測高公式は下から上といった感じです。
この記事では、前回の記事の「全体の流れ」の項目のEとFを扱います。
1.海面更正の式 (E)
1-1. 海面更正とは
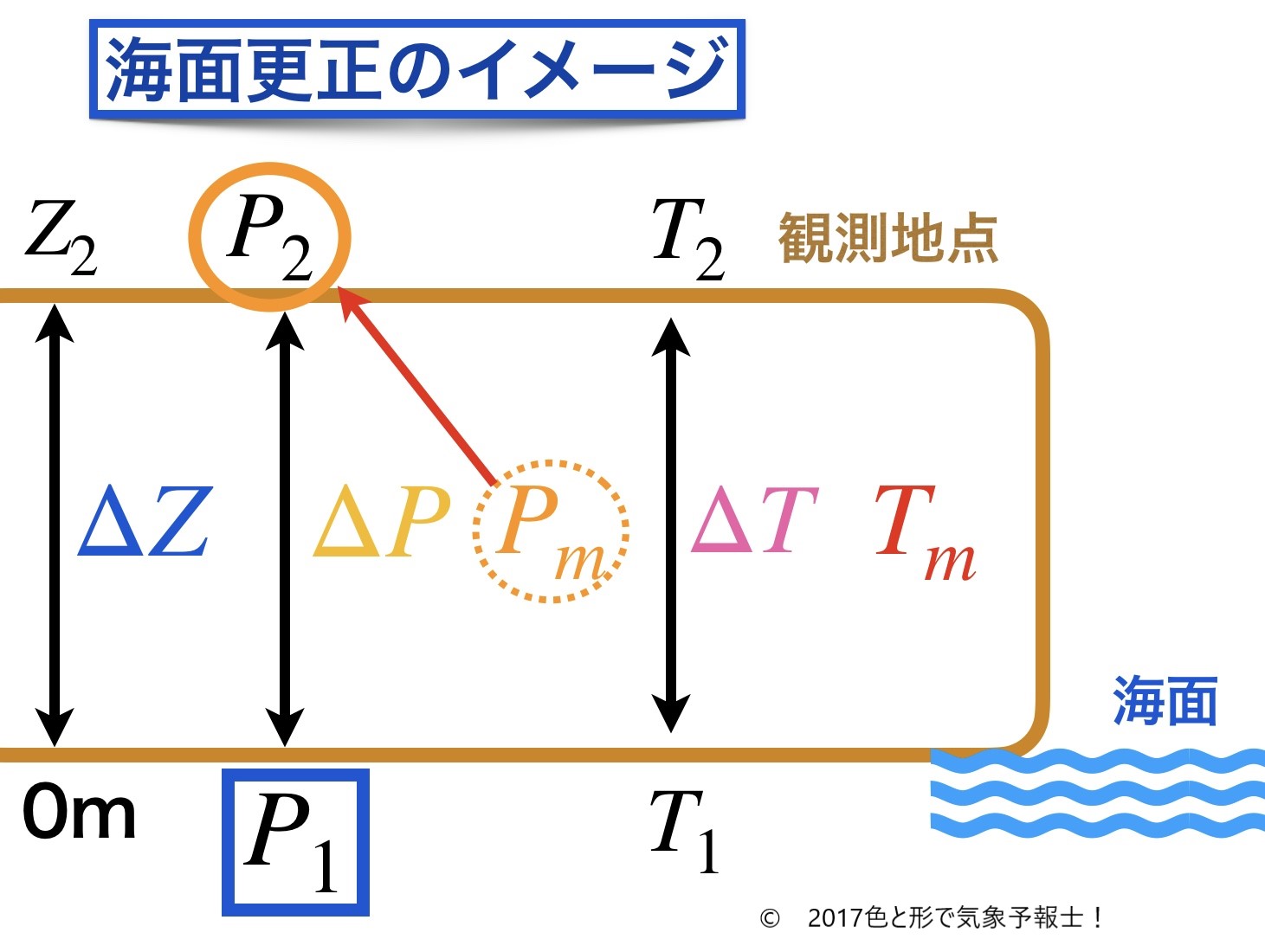
海面更正とは標高が異なる場所で観測された気圧を、高度0m の平均海面高度の海面気圧に換算することをいいます。
気圧は高度が高くなるほど低くなります。例えば、標高500mの山の上にある観測所での気圧が940hPa、海岸近くの標高0mにある観測所での気圧が980hPaだとすると、二つの観測所の間で等圧線はどのように引けるでしょうか?高度を揃えないと分からないですね。
こうした混乱を避けるために海面更正が必要になります。
なお、海面更正が適用できるのは、海抜800m までの観測地点に限られています。
1-2. 海面更正の式の導き方
海面更正は観測した地点の高度と海面高度0mの間を気層とみなして計算します。つまり、気層の上面を観測地点、下面を海面、層厚を観測地の標高として計算する方法です。
ここで、前の記事の復習をします。気体の状態方程式と静力学平衡の式を合体させると次の式が導き出されます。
\(\varDelta P =-\Large{\frac{P}{RT}} \normalsize{\times g\varDelta Z} \) ...(1)
ここで、層厚の式と同様、Pの代わりに平均気圧Pm、Tの代わりに平均気温Tm を用いて変形したのが次の式です。
\(\varDelta P =-\Large{\frac{P_m}{RT_m}} \normalsize{\times g\varDelta Z} \) ... (2)
1-3. 気圧
平均気圧といっても観測地点の下は地中です。それに、そもそも海面高度の気圧を知りたいのだから平均気圧が分かるわけがない。
ということで、平均気圧Pm の代わりに観測地点の気圧P2 を気圧Pとして用いて計算します。
1-4. 気温
平均気温は次の式を利用して仮の海面気温T1を出すことで求められます。
標準大気の気温減率=0.65℃/100m
高度が100m 下がるごとに気温は0.65℃ 上がるということです。こうして
( T1 + T2 ) ÷ 2 = Tm として平均気温を出します。
1-5. 高度差
気層に例えると、この場合、下面の高度は0m 、上面の高度は観測地点の標高になります。ですから高度差ΔZ は観測地点の標高になります。
1-6. 海面更正の式
以上を踏まえて(2)の式に当てはめるとこうなります。
\(\varDelta P =-\Large{\frac{P}{RT_m}} \normalsize{\times g\varDelta Z} \) ... (3)
さらに問題文によっては平均気温を求められていない場合もあるようです。その場合は平均気温Tm の代わりにT2 、つまり観測地点の気温を使うこともできるので、式はさらにこう変形できます。
\(\varDelta P =-\Large{\frac{P}{RT}} \normalsize{\times g\varDelta Z} \) ...(4)
この式は式(1)と同じです。上記の(3)または(4)が海面更正の式となります。
観測地点の気圧P2 と ΔP が分かれば海面気圧P1 も分かります。
1-7.地表付近の気圧変化
地表付近の大気は10m の高度差があると、気圧は約1.2hPa 変化します。これも利用できます。
2.測高公式 (F)
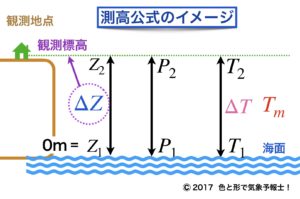
次の測高公式のイメージ図は海面更正の式の図の右側(海側)にあると思ってください。
ここでは海面更正と比べるために海面高度0m の気圧から観測所の標高を求める形にしています。
測高公式は層厚の式を変形することで導き出すことができます。
層厚の式は以下になります。
\(\varDelta Z=-\Large{\frac{RT_{m}}{g}\times\frac{\varDelta P}{P _{m}}}\) ...(5)
この式を自然対数 ln (エルエヌ)で表してみます。
※ 自然対数って何だっけ?という方(私もそうです)は「気象予報士かんたん合格テキスト 学科一般知識編(技術評論社)」の付録の「数学の基礎」を参考にしてください。
\(\varDelta Z=-\Large{\frac{RT_{m}}{g}\times \large ln \Large \frac{P_{1}}{P _{2}}}\) ...(6)
さらに変形して
\( Z_{2} – Z_{1}=-\Large{\frac{RT_{m}}{g}\times \normalsize {(} \large{ln} \normalsize{P_{1}- \large{ln}\normalsize{P} _{2})}}\) ...(7)
上記の式(5)から(7)が層厚の式になります。
また、式(6)、(7)は測高公式といわれる式です。
測高公式の場合、平均気圧の値を用いる代わりに気層の上面の気圧と下面の気圧のそれぞれの値を用いています。
また、上のイメージ図のように、P1 の高度を0m とすれば観測所の標高はΔZと同じになります。こうして気層の平均気温さえ分かれば、気層の厚さを知ることができます。
さらに観測所を上空に当てはめるなら、地上と上空の気圧と温度を測定し、上空の等圧面の高度を知ることができます。こうして高層天気図を作成できます。
3.まとめの数式図
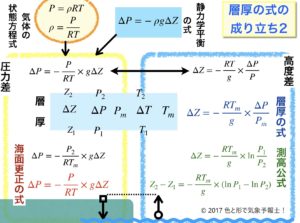
この数式だらけの図は前回の記事でも紹介しました。
静力学平衡の式を応用した3つの式を一つの図にまとめたものです。
次回はまたまた難しいところ。。。
気温減率に取り掛かります 😕