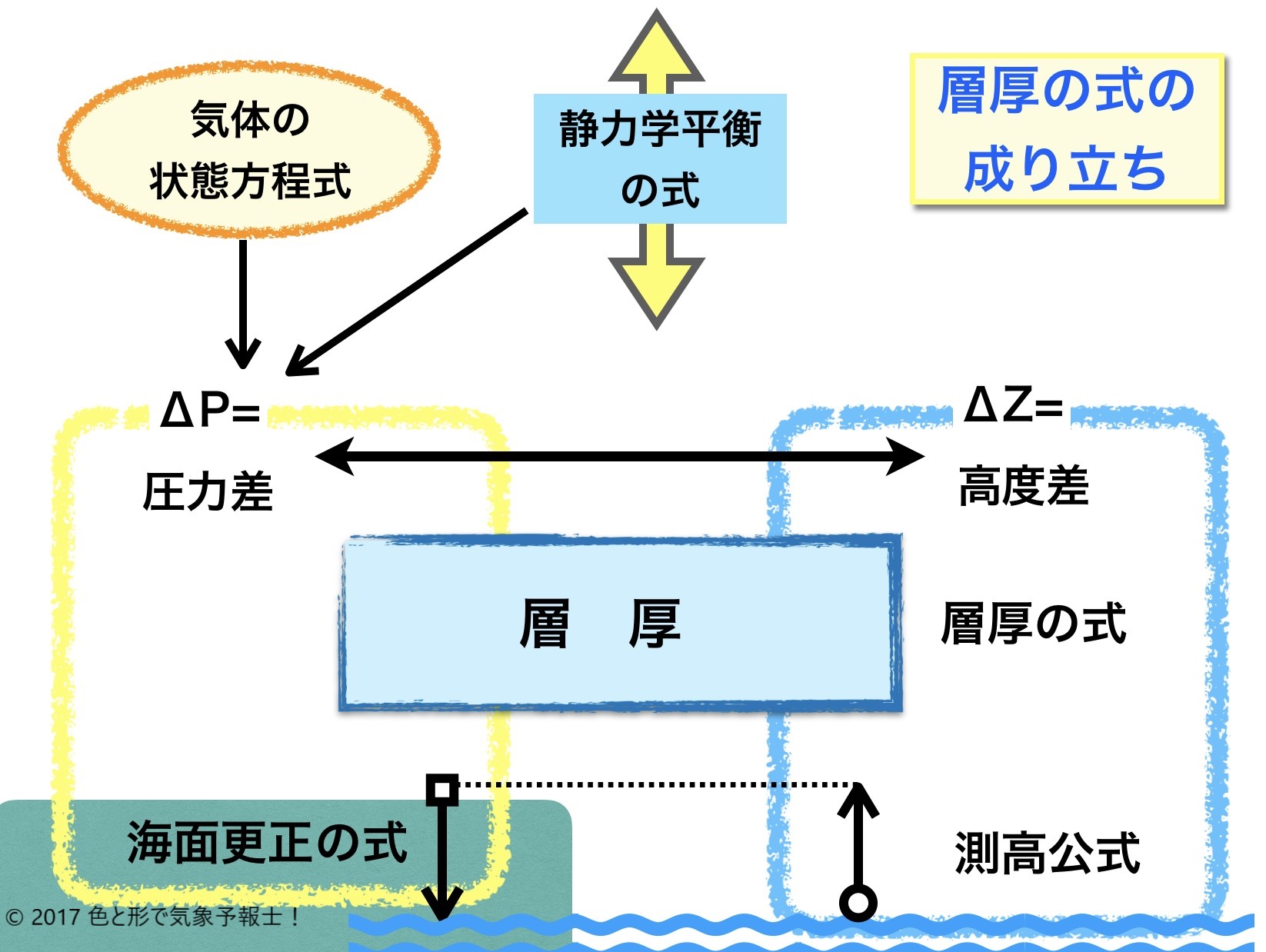
静力学平衡の式を応用すると、層厚の式、海面更正の式、測高公式が導き出されます。
今回は層厚の式の成立ちと意味を考察します。
1.全体の流れ
まずは冒頭のイメージ図をご覧ください。数式は省いた非常におおざっぱな流れを示しています。上から順番に説明します。聞きなれない言葉の意味については後述します。
A 気体の状態方程式と静力学平衡の式を合体させ、圧力差(気圧差)を求める ΔP= の式で示します(左側黄色の枠)。
B その式を高度差 ΔZ= で表す式に変形します。(右青枠)
C ここで層厚を念頭におきます。(中央)
D BのΔZ=の式を層厚に当てはめると層厚の式が成立します。(右青枠内)
E AのΔP=の式を層厚に当てはめると海面更正(海面補正)の式が成立します。(左下)
F 層厚の式を応用して変形すると、測高公式が導き出されます。(右下)
では、AからDまでを詳しく調べてみます。海面更正の式と測高公式は次回に回します。
2.静力学平衡の式と気体の状態方程式の合体(A)
2-1. 気体の状態方程式
左上に気体の状態方程式があります。
気体の状態方程式は圧力、体積、質量、温度の関係を表したものです。
単位体積あたりの質量を密度で表すと、圧力、密度、温度の関係を表しているといえます。
気圧P、密度ρ、気体定数R、絶対温度T とすると、
\(P=\rho RT\) (1)
で表せます。さらに変形すると、こうなります。
\(\rho=\Large{\frac{P}{RT}}\) (2)
2-2. 静力学平衡の式
次に重力加速度g 、高度差ΔZ とすると、静力学平衡の式は次になります。
\(\varDelta P= – \rho g\varDelta Z\) (3)
2-3. 2つの式の合体
式(2)を式(3)に代入して密度を消去すると、気圧差を求める式になります。
\(\varDelta P =-\Large{\frac{P}{RT}} \normalsize{\times g\varDelta Z} \) (4)
でも、どうして2つの式を合体させる必要があるのでしょう?私はこう考えました。
実際の観測で空気の密度を測るのは難しい。標準大気(※)での空気密度は約1.2kg/m3 だが標準大気と合致するケースはあまりない。その点、気圧や温度は簡単に観測できる。ならば、密度を気圧・温度・気体定数に置き換えられる気体の状態方程式を使っちゃおう、という感じでしょうか。
(※)標準大気とは「気温や気圧などの高度分布が、実際の大気の平均状態に近いように単純化した基準大気。」(大辞林第三版の解説)
3.高度差を求める式に変形(B)
(4)の式を高度差を求める式に変形します。
\(\varDelta Z=-\Large{\frac{RT}{g}\times\frac{\varDelta P}{P}}\) (5)
4.層厚とは?(C)
層厚(シネックス)とは、その字の通り、層(気層)の厚さのことで、異なる等圧面間における大気の厚さ、つまり高度差のことです。
例えば700hPa等圧面の高度が3000m、500hPa等圧面の高度が5000mだとすると、高度差2000mが層厚になります。
こちらの記事も参考にしてください ⇒ 「層厚(そして温度風の関係)」
5.層厚の式(D)
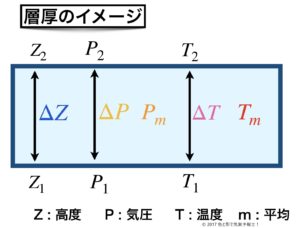
次の図を見てください。
この長方形は気層を横から見たものと考えてください。
知りたいのは層厚(気層の厚さ)の値ですからΔZ を求めればいい訳です。
先ほどの(5)の式を使ってΔZ を求めようとすると、次の疑問がわきます。
● 気圧P はどこの値を用いるか?
● 絶対温度T はどこの値を用いるか?
答えは気層における平均値です。図でいうと、平均気圧Pmと平均気温Tm です。
平均値を用いると(5)の式はこのように変換できます。
\(\varDelta Z=-\Large{\frac{RT_{m}}{g}\times\frac{\varDelta P}{P _{m}}}\) (6)
これが層厚の式です。
この式から分かるように層厚は気層の平均気温に比例します。つまり暖かい大気の層厚は大きく、冷たい大気の層厚は小さいです。
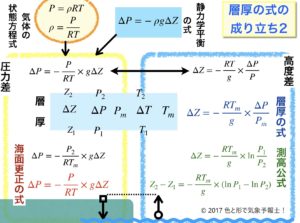
こうした式の変換を整理したのがこの図です。整理した割にはごちゃごちゃしていますね 😉
この図は冒頭の流れの図に数式を記入したものでもあります。
ここまでで図の上半分を取り上げることができました。
次回は静力学平衡の応用として海面更正の式と測高公式についてさらに調べていきます。