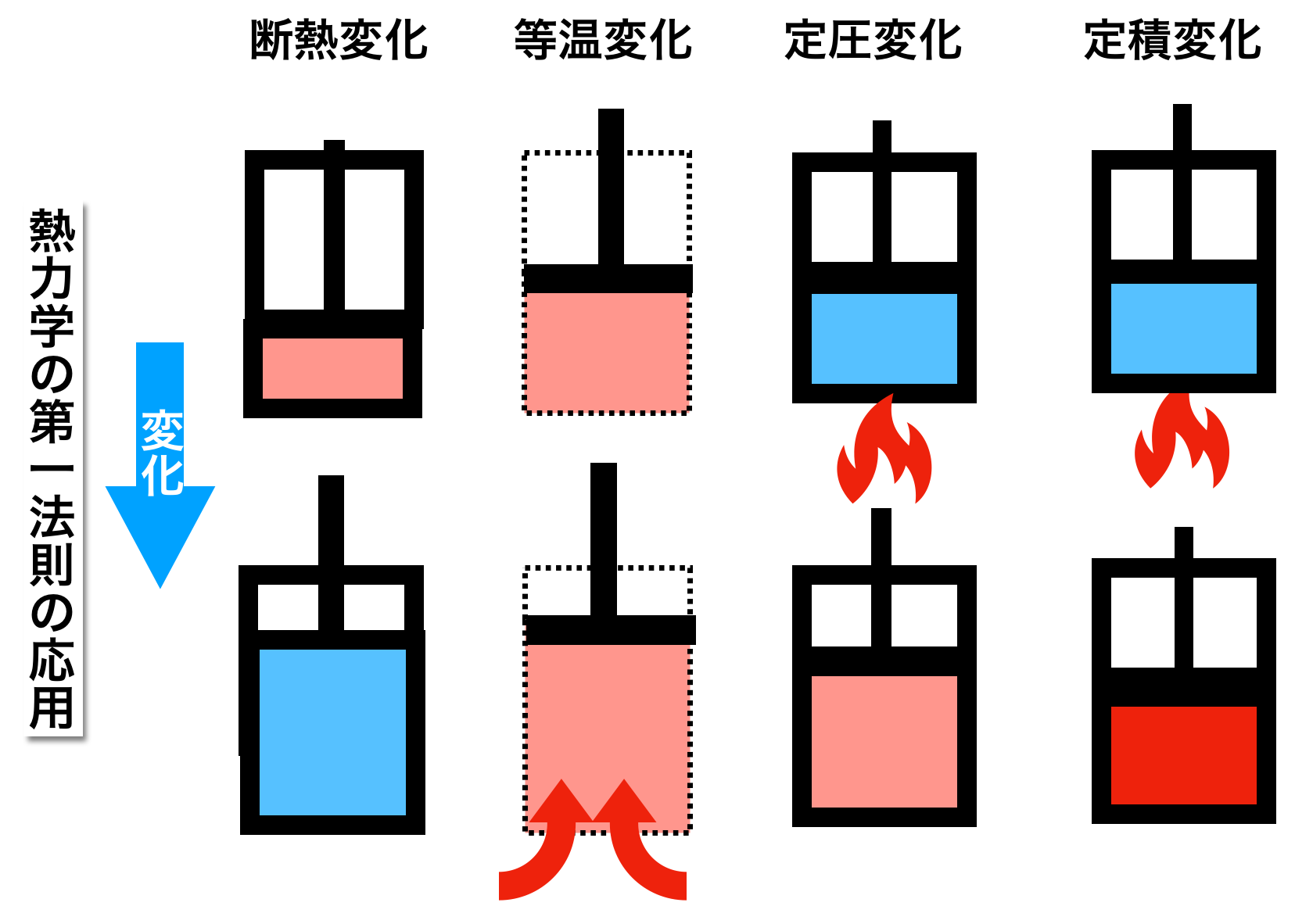
気体の膨張・圧縮、温度の上昇・下降、空気塊の上昇・下降、さらには雲の発生には熱力学の第一法則の応用としての断熱膨張、断熱圧縮といった状態変化が関係しています。
今回は状態変化のうち断熱変化と等温変化について取り上げ、気体の状態方程式との関連も考えます。
目次
1.熱力学の第一法則の復習
ΔQ=ΔU+ΔW
Δ:変化量
Q:気体に加える熱量
U:気体の内部エネルギー
W:仕事に使われるエネルギー量
※ この場合の仕事とは:気体が外部にする仕事
具体的には空気塊が周りの空気を押しのけて膨張するということ
2.仕事の正負と気体の膨張・圧縮
● Wの符号が正(+W)
=外部にする仕事が正
このとき Wの値が大きくなる=膨張する
● Wの符号が負(-W)
=外部にする仕事が負=外部からされる仕事が正
このとき Wの値が大きくなる=圧縮する
3.断熱変化
断熱変化とは、外部との熱のやり取りが行われない状態で空気の圧力、体積を変化させることです。
対流活動のように比較的短い時間で起きる空気の膨張・圧縮が断熱変化に関連しています。
熱力学の第一法則に当てはめると
ΔQ=ΔU+ΔW
ΔQ=0
⇒ 0=ΔU+ΔW
⇒ ΔU=-ΔW
この式から分かるのは仕事エネルギーΔWが増加すれば、その分 内部エネルギーが減少し、逆に仕事エネルギーΔWが減少すれば、その分 内部エネルギーが増加する、ということです。
4.断熱圧縮
4-1. 断熱圧縮とは
断熱圧縮とは、外部との熱のやり取りを行わない状態で気体の体積が小さくなることです。
空気塊が下降するとき、つまり下降気流でこの現象が生じます。
断熱変化の式は以下です。
ΔU=-ΔW
-ΔWは外部からされる仕事、つまり空気塊が外側の空気から押さえ込まれ圧縮するときの仕事エネルギーです。
このエネルギーが増加すると、その分 内部エネルギーも増加します。
ですから、断熱圧縮では空気塊の温度は上昇します。
4-2. ピストンで例えると
上記の図は熱力学の第一法則を応用した4種類の変化をシリンダーとピストンの動きで例えたものです。
一番左のシリンダーが断熱変化を示したものです。
最初(上)容器の中の空気は温度が高い状態でした。そこからピストンを引くと中の空気の体積が大きくなります。同時に空気の温度が下がります。これが次に扱う断熱膨張です。
断熱圧縮は逆にピストンを下から上に変化させたもので、体積が小さくなるにつれ温度が高くなります。
5.断熱膨張
断熱膨張とは、外部との熱のやり取りを行わない状態で気体の体積が大きくなることです。
空気塊が上昇するとき、つまり上昇気流でこの現象が生じます。
断熱変化の式は以下です。
ΔU=-ΔW この式を変形すると
-ΔU=ΔW
ΔWは外部にする仕事、つまり空気塊が外側の空気を押しのけ膨張するときの仕事エネルギーです。
このエネルギーが増加すると、その分 内部エネルギーは減少します。
ですから、断熱膨張では空気塊の温度は低下します。
上昇気流で雲が発生するのは断熱膨張が関係しています。水蒸気を含んだ空気は上昇しながらその温度が低下していき、上空で水蒸気が水や氷の粒となって雲が発生するという仕組みです。
以上まとめると、外部との熱のやり取りがない状態で空気が膨張するとき温度は下がり、圧縮するとき温度は上がるということです。
6.等温変化
等温変化については気象予報士試験にはあまり関係ないかもしれません(と思います)。でも一応調べてみました。
6-1. 等温変化とは
等温変化とは、温度を一定に保ったまま圧力や体積が変化する状態変化をいいます。
温度の高低と内部エネルギーの大小は、関連し合うものなので、等温変化を熱力学の第一法則の式に当てはめると次のようになります。
ΔQ=ΔU+ΔW
ΔU=0
⇒ ΔQ=ΔW
ΔW=PΔV(または ΔW=PΔα)なので
ΔQ=PΔV(またはΔQ=PΔα)となり
体積が増えると熱を吸収し、体積が減ると熱を放出することが分かります。
6-2. ピストンで例えると

左から2番目のシリンダーを見てください。このシリンダーは熱を伝え易い素材で出来ていると考えてください。
上のシリンダーのピストンをゆっくり引くと中の空気の体積が大きくなります。
シリンダーが熱を通しにくい素材で出来ているなら、断熱膨張のように空気の温度は下がっていきます。
でも、このシリンダーは熱を伝え易いので、空気の体積が増えると外から熱を吸収し中の温度が変わることはありません。
逆にピストンを押し込んだ場合は中の熱を外に逃がします。ですから、空気の体積が減ると熱を外に放出するので中の温度が変わることはありません。
このように体積が変化しても気体の内部と外部の温度は等しい状態を保っているというのが等温変化です。
7.気体の状態方程式と熱力学の第一法則の関係
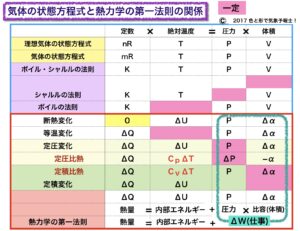
かなり ごちゃごちゃした表を作りました。
これは気体の状態方程式(及びボイル・シャルルの法則)と熱力学の第一法則の、それぞれの変数の関係を表したものです。
この表は、上側(理想気体の状態方程式からボイルの法則まで)と下側(断熱変化から熱力学の第一法則まで)で分かれています。
表の上側では、定数、絶対温度、圧力、体積の列で分けています。
表の下側では、熱量、内部エネルギー、仕事(圧力と比容(体積))の列で分けています。
ピンクの欄は変数が一定あるいは変化なし、を示しています。
8.断熱変化を比容で表す
前の記事で扱いましたが、仕事は 圧力×体積(容積)に置き換えることができます。
さらに体積の代わりに比容を用いて熱力学の第一法則の式に当てはめると
0=ΔU+PΔα
となります。この式の方が気体の体積の変化(膨張・圧縮)と温度変化の関係が分かり易いかと思います。
9.等温変化とボイルの法則
等温変化では内部エネルギーの変化がありません。表でも内部エネルギーの欄がピンクになっていますね。
等温変化の2つ上はボイルの法則の欄となっています。ボイルの法則では絶対温度の欄がピンク、つまり一定だと分かります。ですからこの2つは関連があるといえます。
等温変化 ΔQ=PΔV(またはΔQ=PΔα)
ボイルの法則 PV = K (Kは比例定数で一定)
ボイルの法則には、圧力と体積が反比例するという意味があります。
このように気体の状態方程式(とその基となるボイル・シャルルの法則)と熱力学の第一法則には関連性があることが理解できます。
次回以降で扱う定圧変化、定積変化も同様です。お楽しみに 😉