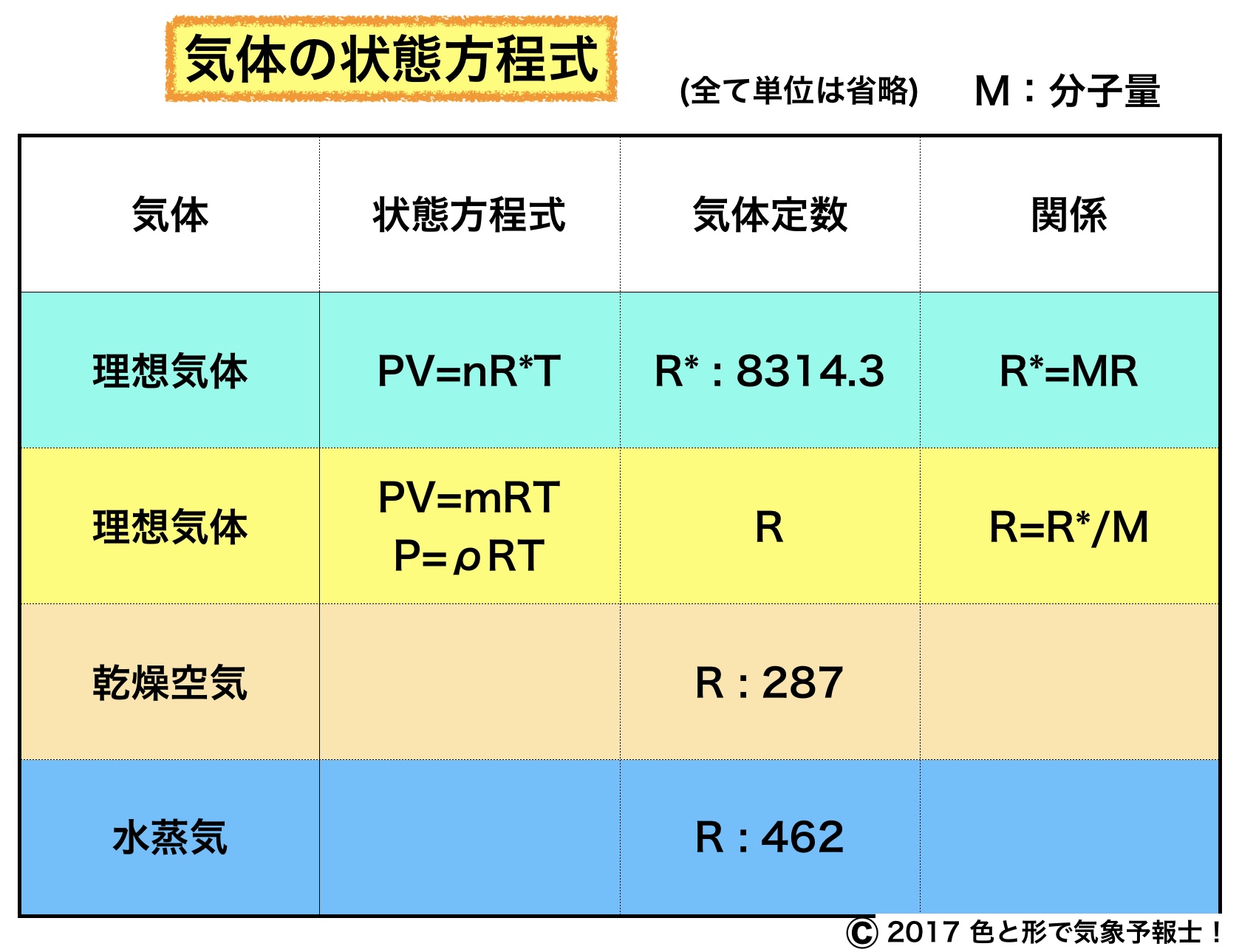
ボイル・シャルルの法則を気体定数を使って表したものが理想気体の状態方程式です。
でも、どこが「理想」なのでしょうか？気体定数とは何でしょうか？
理想気体の状態方程式は熱力学の基礎なので、ここでつまづかないようにしたいですね。（高校で習うみたいですが私はまったく覚えてなかったです 😐 ）
＊もともと１つだった記事が長くなったので、２つに分けました。気体の状態方程式については別記事にしました。
１．これから学ぶこと
過去の2つの記事「気体分子と圧力の関係」、「気体分子と体積の関係」で、下記6項目のうち４項目を取り上げました。今回は５番目の内容を中心に話を進めます。
■ 熱力学にかかわる基本的な用語の確認
■ 圧力を主体にした時の温度、体積、分子数の関係
■ 体積を主体にした時の温度、圧力の関係（ボイル・シャルルの法則）
■ 体積と分子数の関係（アボガドロの法則）
■ 理想気体の状態方程式（←今回の記事）
■ 気体の状態方程式（←後ほど）
２．理想気体とは・・
理想気体とは、ボイル・シャルルの法則が厳密に成り立つ気体のことです。
ボイル・シャルルの法則は、現実には分子自身の大きさや分子間力の影響によって厳密には成り立ちません。そこで、ボイル・シャルルの法則と気体の状態方程式の関係にピッタリ当てはまると仮定した気体を理想気体と呼んで、数値計算や理論の展開を行います。
３．標準状態とは・・
標準状態とは、０℃で１気圧の気体の状態のことです。
４．理想気体の状態方程式と気体の状態方程式の比較
理想気体の状態方程式と後で学ぶ気体の状態方程式の違いを先にまとめてみました。
4-1. 理想気体の状態方程式
PV=nR*T
R*[JK-1kmol-1] : 普遍気体定数（気体の種類に無関係）
n[kmol] : 気体の量 （キロモル）
4-2. 気体の状態方程式
PV=mRT
R[JK-1kg-1] : 気体定数（気体の種類による）
m[kg] : 気体の質量（キログラム）
５．普遍気体定数
5-1. キロモル
気象学では、気体の状態方程式における気体の量mは国際単位系の kmol（キロモル）を利用します。
1kmol=1000mol で、分子数は6.02×1026 個となります。
5-2. 普遍気体定数
計算は省略しますが、ボイル・シャルルの法則から標準状態における気体定数を求めると
8314.3JK-1kmol-1 になります。この数値は気体の種類によらず一定です。
これを普遍気体定数 といい、キロモル比熱ともいわれます。
5-3. 単位換算
〈少し詳細な説明になるので、飛ばしてくださっても構いません。〉
普遍気体定数に J（ジュール）という単位が突然 出て来たように見えますね。
1ジュールとは1 ニュートンの力がその力の方向に物体を 1メートル動かすときの仕事と定義されています。
この場合、ジュールという単位は下記の通り、単位の換算によって出て来たものです。（「気象学における物理量と単位（２）」を参照してください）
PVつまりP×Vを単位を使って表します。
● P ⇒ Pa
Pa=N・m-2=kg・m・s-2・m-2=kg・m-1・s-2
（N=kg・m・s-2)
● V ⇒ m3
● PV＝P×V ⇒ Pa×m3
Pa×m3=N・m-2×m3=N・m=J
（J＝N・m=kg・m2・s-2）
６．理想気体の状態方程式
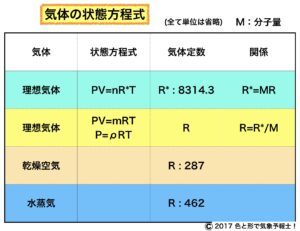
本題に入ります。
■ ボイル・シャルルの法則 PV/T=K を変形すると
PV=KT となります。
また、アボガドロの法則は同温、同圧の下で、全ての気体は同じ体積中に同じ数の分子が含まれる、というものでした。
すると、気体が n[mol] のとき上記の式は
PV=nKT となります。ここで、Kを普遍気体定数R*に置き換えます。すると
PV=nR*T となり、この式を理想気体の状態方程式といいます。
R*をただのRにして PV=nRT としてもいいようです。
■ 上記の式を変形すると
V=nR*T/P となり、同温、同圧のもとでは、気体の体積は気体の種類によらずモル数n（気体の分子数）に依存することが分かります。
■ PV=nR*T を別の形に変形すると
n=PV/R*T となり、同温、同圧、同体積のもとでは、すべての気体で同分子数となることが分かります。
７．まとめ
▶ 理想気体・・ボイル・シャルルの法則が厳密に成り立つ気体
▶ 標準状態・・０℃で１気圧の状態にある気体の状態
▶ 理想気体の状態方程式・・PV=nR*T
▶ 普遍気体定数（R*）・・ 8314.3JK-1kmol-1
乾燥空気や水蒸気など気体の種類の違いに適応した気体の状態方程式についてはこちらをご覧ください。
ではまた、合格に向けて頑張りましょう！