前回は気象を学ぶ上での基礎である 気体の温度、圧力、体積、分子数の関係について、圧力を中心に考えました。
ここからは体積を中心に それらの関係を調べていきます。そして、そこからボイル・シャルルの法則の成立までを考えます。
目次
1.これから学ぶこと
前回の記事では「これから学ぶこと」として以下の6項目を紹介しました。最初の2つは前回学んだので、今回は3番目の内容を中心に話を進めます。
■ 熱力学にかかわる基本的な用語の確認(←前回の記事)
■ 圧力を主体にした時の温度、体積、分子数の関係(←前回の記事)
■ 体積を主体にした時の温度、圧力の関係(ボイル・シャルルの法則)(←今回の記事)
■ 体積と分子数の関係(アボガドロの法則)(←今回の記事)
■ 理想気体の状態方程式(気体の種類によらない式)
■ 理想気体の状態方程式(気体ごとの式)
2.温度、圧力、分子数と体積の関係
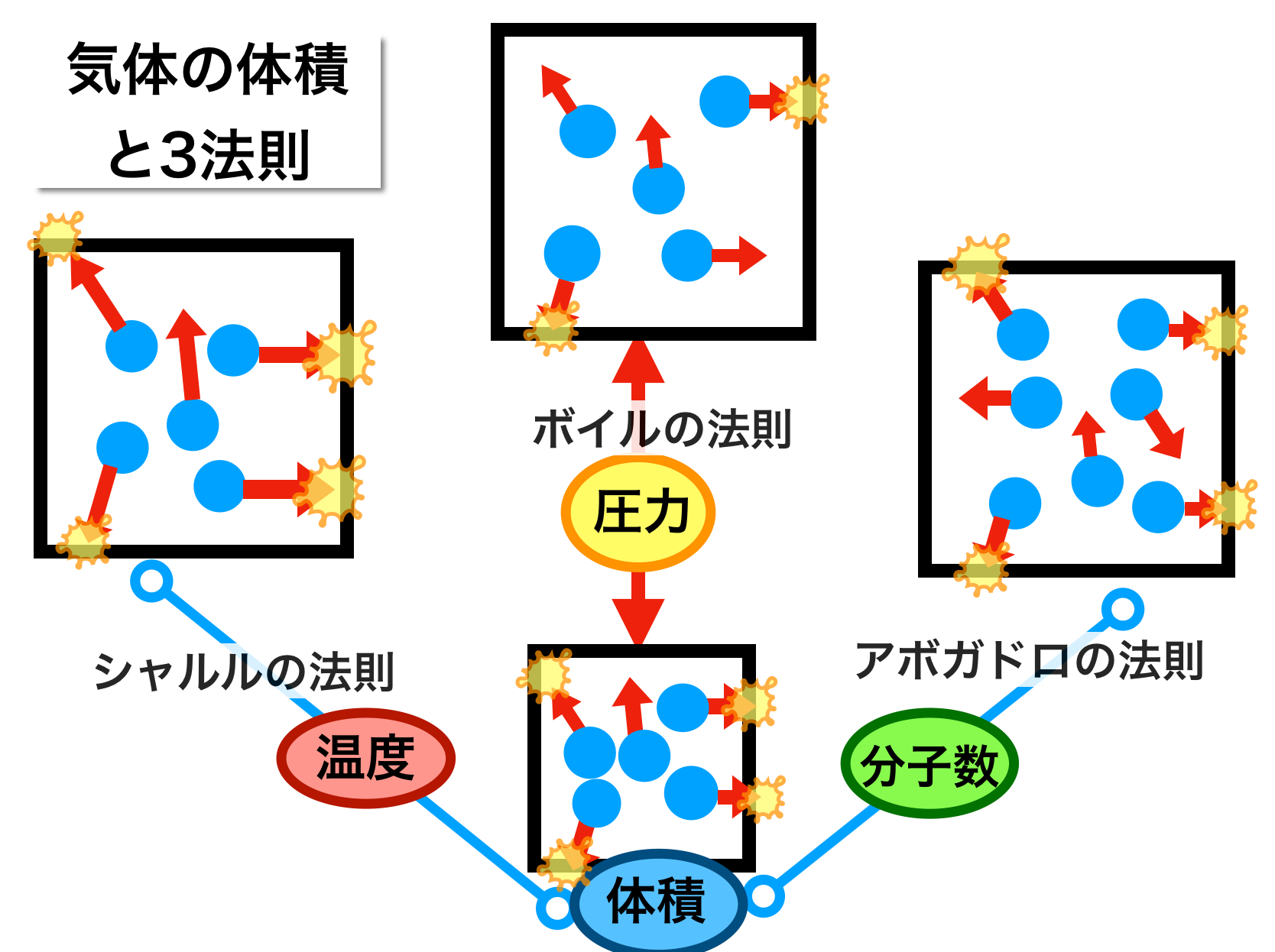
下の図は前回の記事で用いたのと同様の意味のイメージ図です。
体積の変化という観点で見てください。
簡単に図の説明すると、このようになります。(あくまでイメージとして見てください。)
● 四角・・立方体の容器
● 青丸・・空気分子
● 矢印・・分子の熱運動
● オレンジの衝突の数・・圧力の強さ
前回と同じように考えて行くと次の説明が成立ちます。
2-1. 最初の状態(中央の下の容器)
5つの空気分子があり、そのうち4個が壁に衝突して圧力をかけています。
2-2. 体積が大きくなると(中央の上の容器)
温度と分子数が変わらないまま体積を大きくすると、壁に衝突する分子の数が減り、圧力が小さくなります。
逆に体積を小さくする方がイメージし易いかもしれません。
よく使われる例えですが、口をきつく結んだポリ袋の絞ったところをねじっていくと、中の空気の体積が減って袋がパンパンになります。空気の圧力が大きくなったからです。
2-3. 温度が上昇すると(左上の容器)
圧力と分子数が変わらないまま空気の温度を上げると、分子の熱運動が激しくなります。そのため容器の壁は分子に押されて容器自体が大きくなっていきます。つまり体積が大きくなります。
容器は硬いのでイメージしにくいかもしれませんね。代わりに熱気球を想像してみてください。
気球のバーナーに火を付けると気球内の空気が熱せられて膨張し、萎んでいた気球が膨らんで大きくなっていきます。気球内の空気の体積が大きくなったからです。気球内の空気は軽くなり上昇して行きます。
2-4. 体積の違う容器を比べてみると(右上の容器)
温度と圧力が同じ前提では、体積が大きい容器では それだけ 中の分子の数も多くなっています。
例えば体積が2倍だと、中の空気分子の数も2倍になっています。
3.体積を主体にした時の温度、圧力、分子数の比例・反比例関係
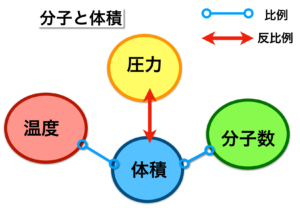
2.で示した例えを基に、分子と体積の関係を比例・反比例で表したのが この図です。
体積と圧力は反比例の関係にあり、体積と温度、体積と分子数は比例の関係にあります。
この関係を踏まえた上で、各法則を見てみます。
4.諸法則で用いられる記号
それぞれの法則について詳しく学ぶ前に関係する要素を表す記号を整理します。
P : 圧力
V:体積
T:絶対温度
K:比例定数
※ PとKは小文字で表す場合もあります。
5.ボイルの法則とは
ボイルの法則・・ 一定の温度の下での気体の体積は圧力に反比例する
この関係を数式で表すと以下になります。
PV = K (Kは比例定数で一定)
ですから気体の体積(V) が2倍になると圧力(P) は2分の1になり、体積(V) が2分の1になると圧力(P) は2倍になります。
圧力の単位は以下が使われます。
◎ N・m-2 と Pa ・・計算に使う
◎ hPa ・・気象学で多用される
6.シャルルの法則とは
シャルルの法則・・ 一定の圧力の下での気体の体積は絶対温度に比例する
この関係を数式で表すと以下になります。
V = KT
※ ボイルの法則のKとシャルルの法則のKは同じ数値とは限らない
7.ボイル・シャルルの法則
ボイルの法則とシャルルの法則を1つにまとめたものがボイル・シャルルの法則です。
ボイル・シャルルの法則・・気体の体積は絶対温度に比例し、圧力に反比例する
この関係を数式で表すと以下になります。
PV = KT
これを変形すると
PV / T = K
となります。
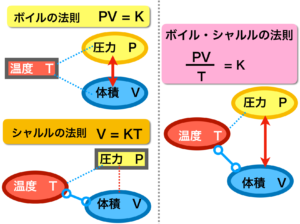
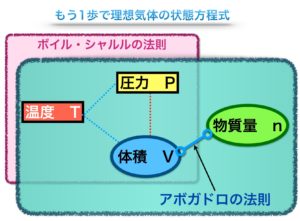
この図は以上の法則を整理したものです。
● 黒い縁の四角・・数値を一定とする
● 楕円形・・数値が変わる
8.アボガドロの法則とは
アボガドロの法則・・同温、同圧の下で、全ての気体は同じ体積中に同じ数の分子が含まれる
言い換えると
気温・圧力が一定の条件下では、体積と分子数は比例する
ということです。
さらに、少し前に取り上げたように物質量(mol) で分子数を表すなら、
気温・圧力が一定の条件下では、物質量 (mol) と体積は比例する
ということになります。
つまり、気体が 2mol あるとき、体積は 1mol のときの2倍になっているということです。
ボイル・シャルルの法則とアボガドロの法則が合体したものが気体の状態方程式の元となります。
ということで、次回は理想気体の状態方程式、気体の状態方程式の理解に挑戦します 😮