気圧と気温は天気予報の必須要素ですね。
でも熱力学で気象を捉える場合、気体の温度、圧力、体積、分子数が必須要素だと理解できます。
体積と分子数を合わせて密度で表すなら、気象学にとって重要なのは、気温、気圧、密度と言うこともできます。
そして それらの要素から「ボイル・シャルルの法則」「アボガドロの法則」「気体の状態方程式」が導き出されます。
1.これから学ぶこと
このブログの初期の頃にも これらの法則を取り上げましたが、ここからはもっと詳しく探っていきます。
それで今回から続く一連の記事で以下の項目を順に取り上げています。
■ 熱力学にかかわる基本的な用語の確認 ←今回の記事
■ 圧力を主体にした時の温度、体積、分子数の関係 ←今回の記事
■ 体積を主体にした時の温度、圧力の関係(ボイル・シャルルの法則)
■ 体積と分子数の関係(アボガドロの法則)
■ 理想気体の状態方程式(気体の種類によらない式)
■ 理想気体の状態方程式(気体の種類ごとの式)
今回は最初の2つの項目に注意を向けます。
2.熱力学にかかわる基本的な用語の確認
用語の正確な定義はかなり専門的になってしまうので、ここでは自分を含め初学者に分かるようにまとめてみました。(「気象学のキホンがよ~くわかる本」などを参考にしています。)
2-1. 熱力学
熱力学・・熱エネルギーのやり取りが関連している理論を集めたもの
2-2. 気体の体積
● 体積(volume)・・物質の空間的な大きさ(V で表す)
● 気体の体積・・気体分子が飛び交っている空間の範囲
● 圧縮・・体積を小さくすること(気体分子の数は変わらないので密度が大きくなる)
● 膨張・・体積を大きくすること(気体分子の数は変わらないので密度が小さくなる)
2-3. 気体の温度
● 温度(temperature)・・熱さ、冷たさを数値で表したもの
◇ セルシウス温度(摂氏)(単位:℃) ⇒ 水が凍る温度を0℃、 沸騰する温度を100℃とする(小文字の t で表す)
◇ 絶対温度(ケルビン温度)(単位:K)⇒ 原子・分子の熱による振動がすべて静止する温度を0℃とする(大文字の T で表す)
◇ 0℃=273K
● 気温・・大気の温度
● 熱運動・・気体内部での気体分子の不規則な運動
分子レベルで見た場合、温度とは分子・原子の熱運動の激しさを表している
2-4. 気体の圧力
● 圧力(pressure)・・物体の表面の面に向かってを垂直に押す力( p で表す)
◎ 1N/m2 = 1Pa (パスカル:圧力の単位)
単位面積(1m2)あたりにに1N(ニュートン:力の単位)の力がはたらいている
◎ 100Pa = 1hPa(ヘクトパスカル)
気象の世界では気圧を表す単位として使われる。
◎ 1013hPa = 1気圧 = 1atm
地上付近の標準的な気圧
3.温度、体積、分子数と圧力の関係
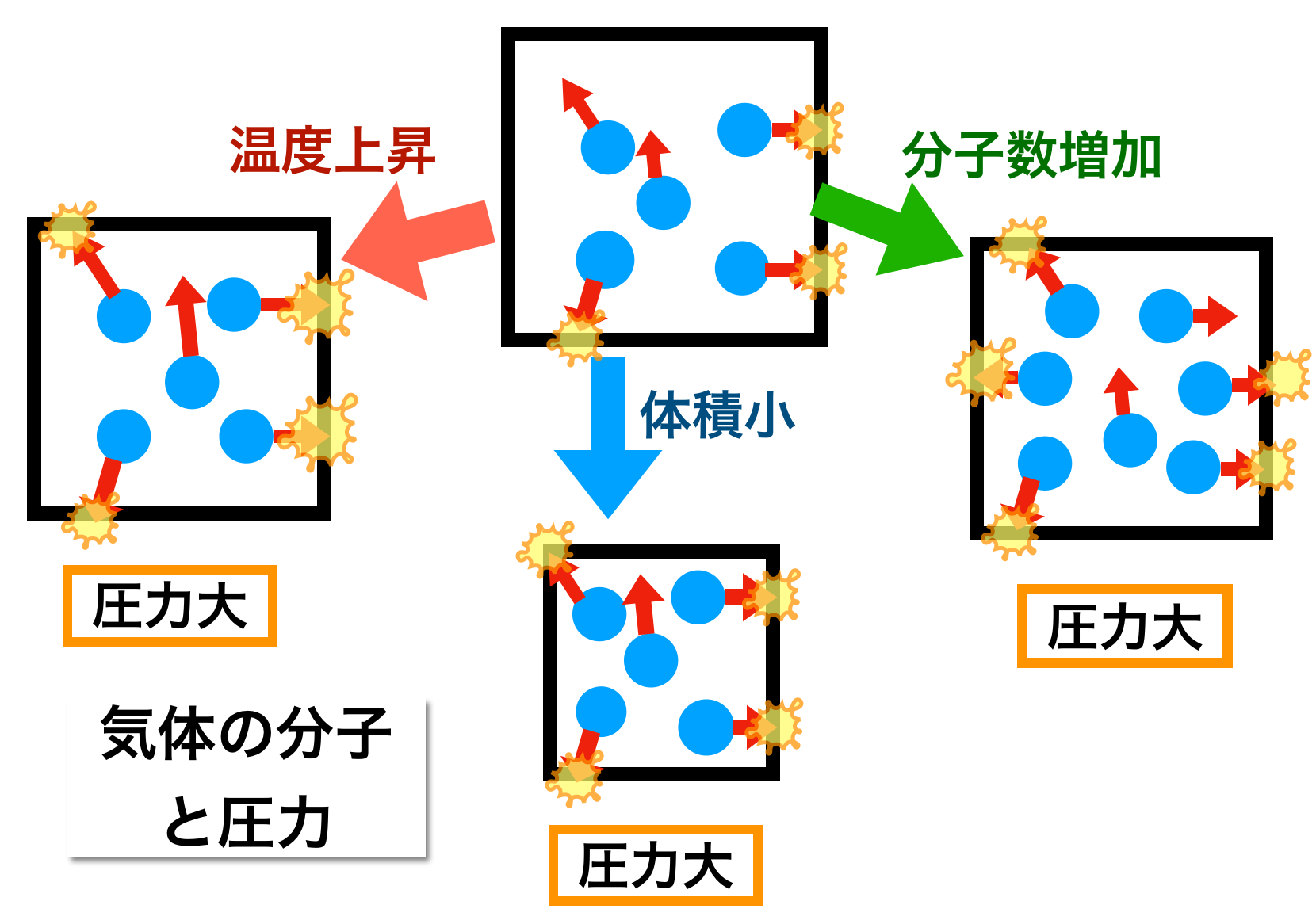
下のイメージ図を説明します。
● 黒い四角・・立方体の容器
● 青丸・・空気分子
● 赤い矢印・・分子の熱運動
● 矢印の長さ・・長いほど動きが活発
● 黄色い印・・空気分子の衝突
壁に衝突する分子の数が多いほど、また その衝突の力が強いほど、圧力が強いことを表現しています。
3-1. 最初の状態(中央の上の容器)
ここに5つの空気分子があり、ばらばらの方向に動き回っています。
容器の壁に3つの分子が衝突し、圧力をかけています。
3-2. 温度が上昇すると(左側の容器)
温度が上昇する、つまり分子の熱運動が激しくなると、壁に衝突する分子の数が増え、衝突の力も強くなるので、容器が受ける圧力は大きくなります。
3-3. 体積が小さくなると(中央の下の容器)
容器の大きさが小さくなると、壁に衝突する分子の数が増え、壁が受ける圧力は大きくなります。
3-4. 分子の数が増えると(右側の容器)
容器の中の分子数が大きくなると、壁に衝突する分子の数が増え、壁が受ける圧力は大きくなります。
4.圧力を主体にした時の温度、体積、分子数の比例・反比例関係
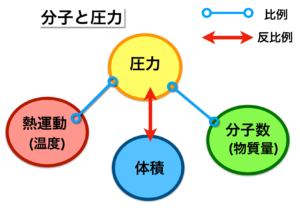
3.で示した例えを基に、容器と圧力の関係を比例・反比例で表したのが、この図です。
圧力と温度、圧力と分子数は比例の関係にあり、圧力と体積は反比例の関係にあります。
ここまで圧力を中心に考えてきました。
一方 体積を中心にして圧力、温度、体積の関係を表現することで、ボイルの法則、シャルルの法則、それらを合わせたボイル・シャルルの法則が導き出されます。
それらについては次回の記事で取り上げます。